今回は、「三角関数と正弦曲線の関係」についての説明です。
1.三角関数と単位円の関係
半径が1になっている円を単位円と呼びます。
x軸y軸の原点O(0,0)を中心とした単位円を描いた時、単位円上にある点の座標について考えます。
突然何の話かと思うかもしれませんが、三角関数についての説明で間違っていないのでとりあえずこのまま読み進めてみてください。
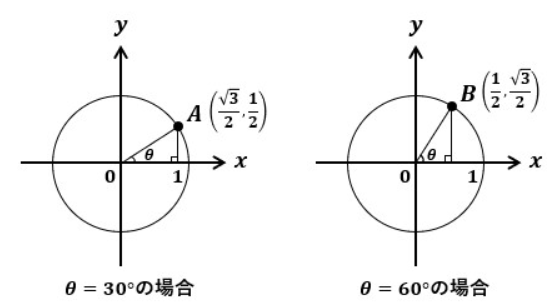
まず、点Aという原点から見て30°の角度の直線と単位円の交点について考えてみます。
点Aからx軸に向けて垂線を引くと直角三角形ができます。
三角比の関係から鋭角30°を持つ直角三角形の各辺の比はわかるので、点Aの座標は(√3/2,1/2)だとわかります。
同様に、点Bという原点から見て60°の角度の直線と単位円の交点について考えると、点Bの座標は(1/2,√3/2)だとわかります。
これらの座標に着目して欲しいのですが、点Aは(cos30°,sin30°)、点Bは(cos60°,sin60°)になっています。
つまり、原点から角度θ方向にある単位円上の座標は(cosθ,sinθ)で表すことができます。
各々を式で表すと、x=cosθ、y=sinθ、y/x=tanθです。
このように円と三角関数には密接した関係があります。
ちなみに、ややこしいので単位円で説明しましたが、半径2の場合は円上の座標が(2cosθ,2sinθ)という具合に等倍になっていくだけです。
また、角度θが0°、90°、180°、270°の時はそもそも直角三角形にならないのでsinとcosの値のイメージがしづらいかもしれませんが、ここで説明したように図示した時の座標を考えるとすんなり理解できるかと思います。
以下の表のようになっていますよね?
| 角度 | sinθ | cosθ |
|---|---|---|
| 0° | 0 | 1 |
| 90° | 1 | 0 |
| 180° | 0 | -1 |
| 270° | -1 | 0 |
2.単位円と正弦曲線
横軸x、縦軸yとした時の単位円にはx=cosθ、y=sinθといった関係式が成り立っていました。
では、θが時間的変化をする時のy=sinθの関係を横軸θ、縦軸yで表してみるとどうなると思いますか?
答えは、図2のような周期的な変化をする波になります。
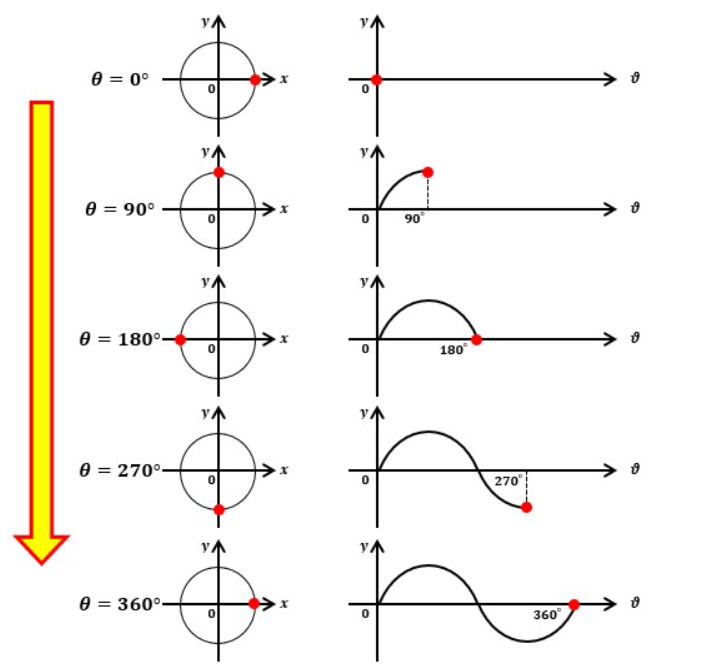
これがいわゆる正弦波・正弦曲線というヤツです。
θが増加していくと、延々と同じ周期の変化を繰り返します。
正弦波は英語で[sine wave]です。
sinの関数は正弦波状になるので、単純にsin波という命名になっているということです。
正弦波・正弦曲線・サインカーブ…呼び方が色々ありますが、指しているものはみな同じです。
電気系を学ぶと交流の分野で基本中の基本として登場するので、そっちへ進もうとしている人はしっかりと理解しておきましょうね。
3.正弦波と余弦波の関係
正弦波より位相(角度)が90°進んでいる波のことを余弦波と呼びます。
sinθに対して角度が+90°になっているということなので、sin(θ+90°)という波形が余弦波となります。
図示すると以下のような違いになります。
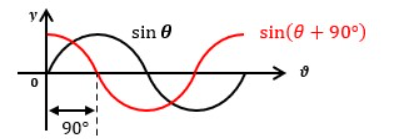
位相がズレているだけで、形状自体は同じです。
余弦波は正弦波に対して位相が+90°になっているだけなので、三角関数と単位円の関係の時のように角度θが0°、90°、180°、270°の場合の座標について表にまとめると以下のようになります。
| 角度 | sinθ | cosθ | sin(θ+90°) |
|---|---|---|---|
| 0° | 0 | 1 | 1 |
| 90° | 1 | 0 | 0 |
| 180° | 0 | -1 | -1 |
| 270° | -1 | 0 | 0 |
表を見てわかるように、sin(θ+90°)とcosθの座標情報は等しくなります。
つまり、sin(θ+90°)=cosθという関係が成り立っているわけです。
以上の関係から、正弦波はsin関数だったのに対して余弦波はcos関数と呼ばれます。
以上、「三角関数と正弦曲線の関係」についての説明でした。




