今回は「将来的な資金計画に役立つ6つの係数の解説(終価係数・現価係数・年金終価係数・減債基金係数・資本回収係数・年金現価係数)」についてです。
目次
１．初めに
普通預金や定期預金には、通常年利が定められています。
年利が高ければ高いほど、数年後に保有している預金額が増えていきます。
この辺りの原理は前々回の記事にまとめてあるので、気になる方は以下を参照してください。
簡単に説明すると、もし仮に100万円を年利1%の定期預金に入れていた場合、1年後には100万×1.01=101万に増え、2年後には101万×1.01=102万と100円になります。
年数を重ねると、増えた資産に年利が掛かってくるので、利益が少しずつ積み上げられて増えていくんですよ。
このような、「年利何%で運用したら10年後にはどの程度まで資金が増えるのか」という計算の他にも、「この金額を10年後に得るためには毎年どの程度の積み立てが必要なのか」など、将来のことを考えて計算しておきたいことってよくあるんですよね。
これらの資産形成に関わる計算に関する代表的な係数が6つあります。
今回は、そんな資産計画に役立つ6つの計算式・係数について解説していきます。
２．資金計画に役立つ6つの係数
資金計画に役立つ6つの係数は、以下の種類があります。
- 終価係数
- 現価係数
- 年金終価係数
- 年金現価係数
- 減債基金係数
- 資本回収係数
それぞれ何を表す係数なのかを説明し、計算式と例で以って解説していきます。
ただ、FPの試験に出てくる内容は、説明文に該当する係数を選択したり、表記されている係数から適切なものを使用して元本や元利を計算させるような問題しか出てきません。
なので、試験合格を考えるだけなら計算式まで覚える必要は無かったりします。
私は備忘録としてまとめておくことが目的なので、係数の計算式の求め方まで全部説明していますが、どこまで知りたいのかで適度に読み飛ばしていただければと思います。
実際の計算に用いることが可能な係数(数値)の一覧表・早見表に関しては後程の項にまとめて載せますので、まずは各解説からです。
元本・元利・元金・複利の意味
6つの係数の解説に入る前に、投資金額などを指す基本的な用語をいくつか解説しておきます。
読み方も微妙にわかりづらく、似たような意味・字面の用語が多いので、一ヵ所にまとめた方がいいかなと思いまして…。
“がんぽん”と読みます。
金融取引や投資で最初に投入したお金のことです。
初期投資額のことですね。
“がんり”と読みます。
元金と利子/利息の合計のことです。
元のお金に対してどれぐらい増える/減るのかを計算した結果ということです。
最終的に係数から求めたい結果が大体元利に当たります。
“がんきん”もしくは“もときん”と読みます。
貸し借りした元のお金のことです。
若干ニュアンスが異なることもあるようですが、ほぼ元本の同意語だと思ってください。
元本に利息を再投資して計算に含める運用方法のことです。
銀行の例で、年利1%で2年経過した場合に得られる金額を計算する際、1年経過時点で発生している利息1万円を加えた101万を元本として計算していたでしょう？
アレが複利計算です。
複利は、投資でよく言われている「利息が利息を生む仕組み」・「お金がお金を稼いでくる仕組み」を構築するための手段に成り得ます。
時間が経つほど資産が加速度的に増える計算になるので、夢が広がるんですよね。
終価係数とは？(＋複利の説明)
元本を複利で運用して、将来的に得られる元利を求めるための係数です。
先程例に挙げたような、銀行に預けた金額が数年後には何円になっているのかを計算する時なんかに使う係数です。
終価(しゅうか)とは、元本を一定期間・一定利率で複利運用した時に、将来的にいくらになるのかを表す将来価値のことです。
終価を求める係数という単純な名称になっているわけですね。
終価係数の計算式は、以下の通りです。
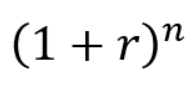
rが年利などの利率、nが年などの期間です。
大体は年利と経過年数で計算することになります。
例えば、投資信託でS＆P500やオルカンなどに一括で100万円突っ込んで10年間放置したら、10年後にはどの程度の資産になっているのか気になりませんか？
これらの投資信託は過去の傾向から年利5%～7%程度の期待が持てますので、年利5%で計算すると100万円×(1+0.05)10≒163万円になります。
年利7%なら、100万円×(1+0.07)10≒197万円です。
つまり、100万円を10年放置しておくと、60～100万円増えてるかもしれないのです。
元本がほぼ2倍になるんですよ。
もし元本が1,000万円だったら、10年で2,000万円も夢ではないというわけです。
もちろん、バブル崩壊・リーマンショック・ブラックマンデーのように株価暴落のリスクはありますし、数年の短期スパンだと寧ろ減ることもありますし、年利5%～7%程度というのも過去の傾向から導いた予想でしかありません。
それでも、計算通りに上手くいく可能性もあるのですよ。
このような複利による利益の計算に、終価係数が使われるというわけです。
ちなみに、2025年3月～11月までS&P500を積み立てNISAで放置したところ、18%増加していました。
下振れすることもありますが、しっかりと上振れすることもあるのです。
現価係数とは？
一定期間後に得られる金額を現在の価値に換算するための係数です。
言い換えると、将来的に一定金額を得るためには現在いくらの元本が必要になるのかを逆算するための係数です。
現在必要な価格を求める係数と覚えましょう。
例えば、5年後に400万円の車を買いたいと考えていたとして、ローンは組まずに一括で払いたかったとします。
車の購入資金を貯めるためにS&P500やオルカンに一括で突っ込んでおこうと考えましたが、5年後に400万円貯めるためには今どの程度の元本があれば良いのでしょうか？
仮に年利5%で複利運用されると考えると、少なくともS&P500やオルカンに突っ込む金は(理論上は)400万円以下になっているはずですよね？
そんな計算をする際に役立つ係数が現価係数というわけです。
さて、この計算についてよく考えてみてください。
終価係数とは逆のことをやろうとしていることがわかりますか？
終価係数は、複利で運用したら今現在の資産がどこまで膨れ上がるのかを計算するための係数でした。
それに対して現価係数は、目標金額を入手するには複利で運用するとして現在の資産がいくらあれば良いのかを計算する係数です。
見事に求めるものが逆転しているんですね。
さて、肝心の現価係数の計算式ですが、説明されるまでもなく予想が付くのではないでしょうか？
そう、終価係数の逆数が現価係数です。
現在の資産に終価係数をかけると未来の予想資産が求められて、未来で必要になる資産に現価係数をかけると現在必要な資産が求められます。
言い方を変えると、現在必要になる資産を現価係数で割ると未来で必要になる資産が求まるわけですからね。
ということで、現価係数の計算式は以下の通りです。
rが年利などの利率、nが年などの期間です。
先程の例のように、年利5%の複利運用して5年後に400万円を用意したかったとします。
この場合、400万円×{(1/1+0.05)5}≒313.4万円となり、S&P500やオルカンには315万円程度入金しておけば5年後には大体400万円になると算出できるわけです。
あくまで順調に増えた場合のシミュレーション値ですが、今現在どの程度のお金が必要なのかという指標にはなるでしょう？
年金終価係数とは？
定期的に一定金額を積み立てて、一定期間経過した際の元利合計額を求めるための係数です。
要するに、積み立て金額の合計と、積み立てた金によって得られる利益を足し合わせたものを求めるための係数が年金終価係数となります。
具体例を挙げると、積み立て投資をした際の将来的な元利合計を計算するのに年金終価係数が有用なのだと思ってください。
例えば、毎年10万円を年利5%で5年間積み立て投資したとします。
積み立てNISAでS&P500とかオルカンを買って気絶を決め込んでいる人達の運用イメージですね。
年金終価係数の計算式は以下の通りです。
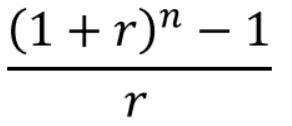
rが年利などの利率、nが年などの期間です。
この辺りから式の見た目が厳つくなってきます。
計算式に当て嵌めると、年金終価係数は{(1+0.05)5－1}/0.05≒5.53になるとわかります。
毎年10万円積み立てる設定なので、10万円×5.53≒55.3万円が5年後の元利だということがわかります。
年利5%で10万円を5年間積み立てると、5年間放置するだけで約5.3万円増えるのです。
年金終価係数の計算式の求め方についても説明していきます。
毎年一定額のX円を年利r%でn年間積み立てていきます。
最初の年に積み立てたX円はn年後まで運用されるので、n－1回分の利子が繰り返し付きます。
2年目に追加で積み立てたX円はn－1年後まで運用されるので、n－2回分の利子が繰り返し付きます。
これをn年後まで繰り返すと、最終的に以下のように計算できます。
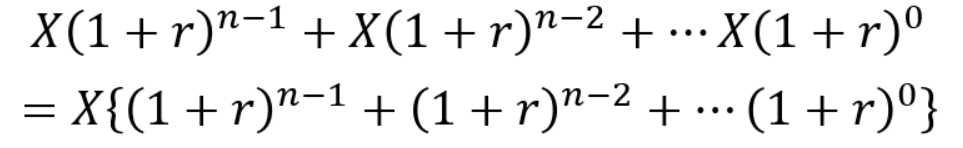
この中括弧{}内の計算ですが、等比数列になっています。
この等比数列の和には公式があり、初項がA、公比(比率)がR、項数がNの時、以下のようになります。
この等比数列の和の公式に式4の中括弧内部{}を当て嵌めて考えると、初項A=1、公比がR=1+r、項数N=nになっていることがわかるでしょうか？
従って、式4の中括弧内部{}は、等比数列の和の公式より、以下のようになります。
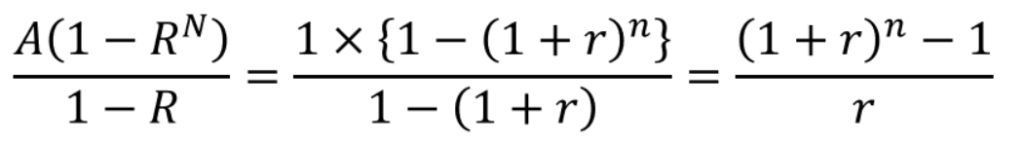
毎年の積立金額X円に対して式6をかければ、年利r%でn年間積み立てた場合の元利合計額が求まるわけです。
なので、式6を年金終価係数としているというわけです。
減債基金係数とは？
将来的に一定金額を得るために必要になる定期的な積み立て額を計算するための係数です。
積み立て投資をした際の将来的な元利合計額の目標値に対して、具体的に何年間に渡って毎年何円投資すれば良いのかを求める際などに有用な係数です。
つまり、年金終価係数と逆のことをするための係数が減債基金係数というわけです。
終価係数と逆のことをしているのが現価係数でしたが、今度は年金終価係数の逆のことをしているのが減債基金係数なのです。
名称が対になっていないのと、後述の年金現価係数の存在により、ちょっとわかりづらくなっています。
さて、減債基金係数の計算式ですが、年金終価係数と逆のことをするだけなので、年金終価係数の逆数になっています。
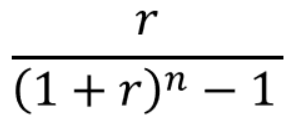
rが年利などの利率、nが年などの期間です。
例えば、年利5%で5年間積み立てをして、5年後には200万円を貯めておきたかったとします。
この場合の減債基金係数は、0.05/{(1+0.05)5－1}≒0.18となります。
つまり、5年後の目標金額200万円にこの減債基金係数をかけることで、年間積立必要金額を求めることができます。
200万円×0.18=36万円。
よって、毎年36万円程度を積み立てれば、5年後に200万円くらいになるというわけです。
資本回収係数とは？
現在の元本を一定利率で運用しつつ一定期間で取り崩す際の毎年の受領額を計算するための係数です。
老後の終活で元本に対して毎年何円切り崩して使っても大丈夫なのかを計算したり、住宅ローンを組んだ際に毎年何円返済していけばローンを返済できるのかをシミュレーションするために使える係数となります。
ここまで解説してきた係数にも言えるのですが、受給ではなく返済の場合にもこれらの係数は使えるんですよね。
受け取る側と受け渡す側とで視点が変わるだけなので、当たり前のことではあるんですけどね。
資本回収係数の計算式は以下の通りです。
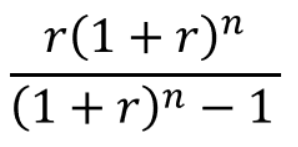
rが年利などの利率、nが年などの期間です。
さて、資本回収係数の求め方ですが、これまで解説してきた係数について理解していれば導き出せるようになっています。
というか、以下のように分解すればわかります。
はい、終価係数×減債基金係数になっているんですね。
何故こうなっているのかは、よく考えればわかります。
現在の元本を一定利率で運用しつつ一定期間で取り崩す際の毎年の受領額を計算するための係数が資本回収係数なわけですが、現在の元本を一定利率で運用せずに一定期間で取り崩す際の毎年の受領額を計算するための係数は減債基金係数なんですよ。
減債基金係数を使えば将来的に一定金額を得るために必要になる定期的な積み立て額を計算できるので、逆に言えば将来的に一定金額を返済するために必要になる定期的な返済金額を計算できるわけですからね。
先程述べたように、各係数は返済や取り崩しの考え方にも適用できるのです。
そして、元本を一定利率で運用して将来的に得られる元利を求めるための係数がありましたよね？
そう、終価係数です。
つまり、終価係数(現在の元本を一定利率で運用する)×減債基金係数(一定期間で取り崩す際の毎年の受領額を計算する)=資本回収係数という関係になっているわけです。
例えば、100万円を年利5%で借りて10年で完済を目指している場合、資本回収係数は0.05(1+0.05)10/{(1+0.05)10－1}≒0.1295となります。
なので、100万円×0.1295で12万5千円を毎年返済していれば、10年後には100万円の返済が可能となるわけです。
総返済額は125万円となるため10年で25万円余計に払わされていますが、これがローンというものです。
住宅ローンは仕方ないとして、できる限りは一括払いをできる範囲で買い物をするか、頭金を多めに払っておくと良いですよ。
まあ、5%も年利をかけてくることは無いとは思いますけどね。
参考として、私が保有している不動産の年利は1.975%となっています。
年金現価係数とは？
元本を複利運用しつつ毎年一定金額を取り崩すために必要となる元本を求めるための係数です。
老後の終活で年間200万使いたかったとして、元本はいくら用意しておけば年200万ずつ取り崩しても大丈夫なのかを計算する際などに使えます。
ここまでの流れでわかるかと思いますが、資本回収係数の逆のことをするための係数が年金現価係数です。
年金終価係数の逆ではない点に注意が必要です。
名称がややこしいんですよ。
さて、年金現価係数の計算式ですが、資本回収係数と逆のことをするだけなので、資本回収係数の逆数になっています。
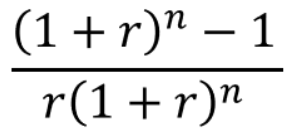
rが年利などの利率、nが年などの期間です。
そして、終価係数×減債基金係数=資本回収係数だったので、それぞれの逆数に置き換えることでも式は成り立っています。
要するに、現価係数×年金終価係数=年金現価係数になっています。
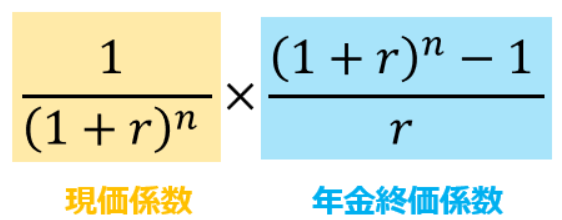
例えば、元本を年利5%で複利運用しつつ毎年200万円を10年間の間取り崩していきたかったとします。
この場合、{(1+0.05)10－1}/0.05(1+0.05)10≒7.7217となります。
なので、200万円×7.7217≒1,544万円程度用意しておく必要があるとわかります。
老後資金を積み立てNISAから切り崩していく際などに役に立つ係数というイメージで良いかと思います。
ちなみに、式10は整理すると以下のようになるので、見た目的にはこちらの方がスッキリします。
ただ、パッと見で資本回収係数の逆数にならなくなってしまうので、混乱しそうなんですよね。
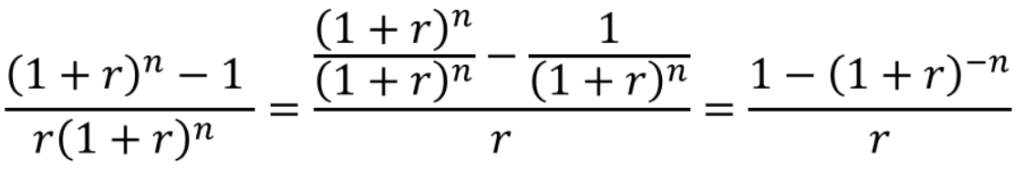
３．6つの係数の関係まとめ
資金計画に役立つ6つの係数を一つ一つ詳しく解説してきたので、ここで一旦内容をまとめようと思います。
それぞれの係数の大まかなイメージ分けをすると、以下のようになります。
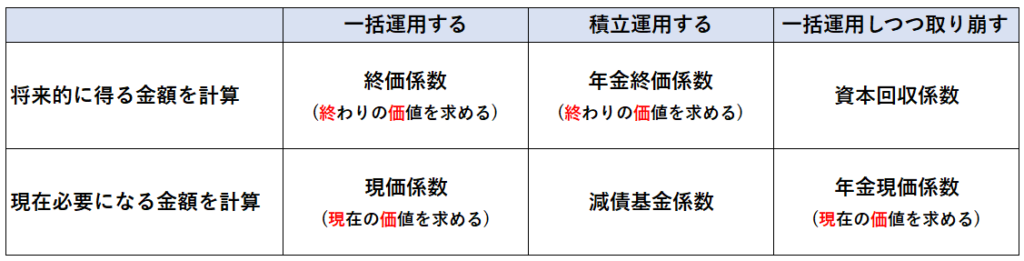
こうしてみると割とスッキリしているんですよね。
終価という名称になっている係数は終わりの価値(一定期間後の金額)を求めるための係数で、現価という名称になっている係数は現在の価値(今必要な金額)を求めるための係数になっています。
6つの係数は将来的に得る金額=終価と現在必要になる金額=現価のどちらかを求める係数なので、表の配置と名称がある程度関連付けされます。
また、減債基金係数は減債(負債・借金を少しずつ減らすこと)と基金(特定の用途にあてるための資金)の係数なので、借金を少しずつ分割して返済していくための資金を求める係数だと想像できます。
なので、表の下段の行の[現在必要になる金額]であることが想像できます。
資本回収係数も資本(事業などを行うための元手)を回収する係数なので、少なくとも現在必要になる金額を求める係数ではないことは名称から連想できるかと思います。
なので、表の上段の行の[将来的に得る金額]であることがわかります。
そうなると、自ずとどの係数が表のどの位置に該当するのかは結びついてくるんですよね。
ということで、用語単体で暗記しようとせず、このような表の形で6つの係数まとめて覚えてしまった方が良いかと思います。
４．各係数の早見表
ここまで説明した内容からわかる通り、どの係数も年利と経過年数によって変化するものとなっています。
なので、実際に計算する場合は、“年利何%の状態で経過年数を何年の時”という条件付けをして各係数の計算を行う必要があります。
ただ、毎回そんなことするのは面倒ですよね？
時が経てば各係数の計算式なんて普通に忘れるでしょうし。
ということで、実際に計算する場合は、“年利何%の状態で経過年数を何年の時”という条件付けをした早見表を用意しておき、そこから必要な係数を読み取ることが多いです。
FP3級の過去問でも、どの係数を使用する必要があるのかを判断した上で、表記されている係数値を以って計算するという問題はよく出てきます。
参考として、ここでは年利1%・3%・5%で経過年数は10年間までに対応させた係数表を載せておこうと思います。
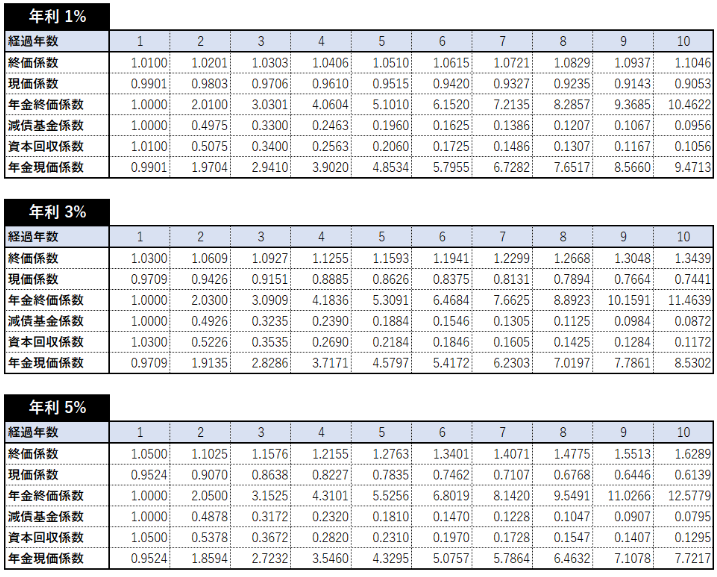
例えば、終価係数の説明で100万円を年利5%で10年放置したら約163万円になると述べましたよね？
年利5%で10年経過させた場合の終価係数は1.6289なので、100万円×1.6289≒163万円と計算できます。
同じ答えになっているでしょう？
こんな感じで早見表を使用するわけです。
本質的な理解をするなら係数の計算式も重要ですが、ファイナンシャルプランニングに求められているのは係数値ですからね。
早見表で充分なんですよ。
以上、「将来的な資金計画に役立つ6つの係数の解説(終価係数・現価係数・年金終価係数・減債基金係数・資本回収係数・年金現価係数)」についてでした。
