今回は、「等比数列の和の公式の求め方」についての説明です。
1.初めに
本ブログでは等差数列と等比数列の違いをまとめています。
この内の一つの等比数列(隣り合う数字の比が等しくなっている数列のこと)についてなのですが、そのすべてを合計した和の公式というものが存在します。
FP(ファイナンシャルプランナー)に関わる内容をまとめている際に、その等比数列の和の公式の理解をしていないと本質的な部分まで解説ができなかったので、こうしてまとめておこうとしています。
具体的には、年金終価係数の求め方に等比数列の和の公式が必要でした。
年金終価係数は、定期的に一定金額を積み立てて、一定期間経過した際にどれだけお金が増えているのかを計算するための係数です。
割と重要な計算式のために使われているんですよ。
まあ、教材にはその肝心の年金終価係数の求め方は書かれておらず、計算結果だけ書かれていることが多いのでこんなことになっているわけですけども…。
キングクリムゾンかな?
2.等比数列の和の公式
初項がA、公比(比率)がR、項数がNになっている等比数列があった場合、等比数列の和の公式は以下のようになります。

この公式は、公比R≠1の時に成り立ちます。
公比R=1の場合は初項Aが項数Nだけ加算されるだけなので、ANが等比数列の和となります。
今回は、この公比R≠1の時の等比数列の和の公式の求め方を説明していくことになります。
3.等比数列の和の公式の求め方
等比数列の和Snから等比数列の和Snに公比Rをかけたものを引き算してみます。

すると、いい感じに打ち消し合って、大分スッキリします。
ここから式を変形していきます。
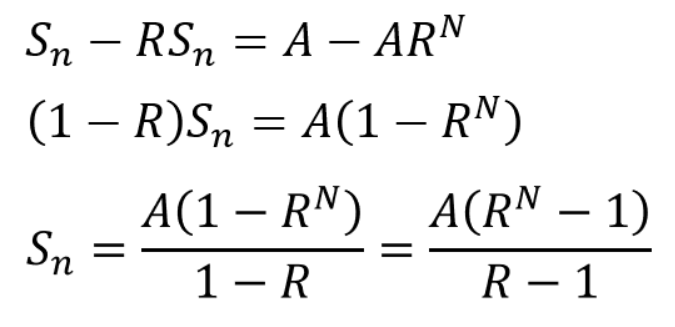
はい、これだけです。
数学の公式全般に言えるのですが、最初の発送が突飛なだけで、一度理解してしまうと簡単なものって多いんですよね。
以上、「等比数列の和の公式の求め方」についての説明でした。



