【基礎から学ぶコンデンサ】平行板コンデンサに導体を挟んだ場合の静電容量

“コンデンサ”という部品は、電気製品なら必須レベルで多用されています。
電気を蓄えたり放出したり、ノイズ成分を吸収したり、何かと便利だからです。
本記事では、そんなコンデンサという部品についての知識をわかりやすくまとめてみました。

今回は、「平行板コンデンサに導体を挟んだ場合の静電容量」についての説明です。

平行板コンデンサの静電容量

平行板コンデンサの静電容量C[F]は、誘電率ε[F/m]と導体板の面積S[m²]に比例し、導体板間の距離d[m]に反比例する。

平行板コンデンサに導体を挟んだ場合の静電容量

導体の長さをx[m]とすると、以下のようになる。
平行板コンデンサの静電容量C[F]は、誘電率ε[F/m]と導体板の面積S[m²]に比例し、導体板間の距離d-x[m]に反比例する。

コンデンサには電荷を蓄えられる容量があり、これを静電容量と呼びます。
量記号はC、単位は[Fファラド]です。
コンデンサについての詳しい説明が必要な方は先に以下の記事を読んでみてください。

コンデンサは、2枚の金属板が並んだ構造になっていて、金属板の間には誘電体(絶縁体)が挟まれています。
その為、平行板コンデンサ、平行平板コンデンサとも呼ばれています。

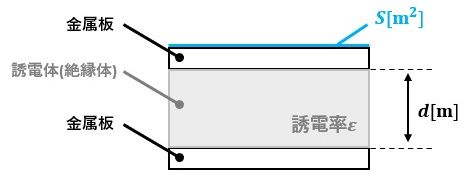
平行板コンデンサの静電容量C[F]は、誘電率ε[F/m]と導体板の面積S[m²]に比例し、導体板間の距離d[m]に反比例します。

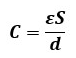
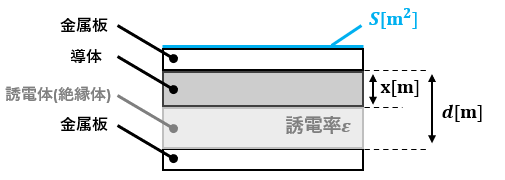
ここからが本題、『この平行板コンデンサに導体を挟んだら静電容量はどうなるか』です。

結論から言います。

導体の長さをx[m]と置いた時、
C=εS/dという関係式の内、dがd-xに置き換わるだけです。
つまり、C=εS/(d-x)です。

導体の誘電率について考えだすと理解に苦しんですごいことになると思うので、ここでは置いておきます。
単純に金属板が分厚くなって平行板距離がx[m]分短くなっただけというイメージで覚えてしまいましょう。
※ 覚えるためのイメージの話です。

図2のように導体と誘電体で二分されている場合はもちろん、誘電体と誘電体の間に導体が挟まれていたとしても同じことが言えます。

以上、「平行板コンデンサに導体を挟んだ場合の静電容量」についての説明でした。