今回は、「カルノー図を用いた論理式の簡単化」についての説明です。
1.ポイント
カルノー図を使うと、論理式を綺麗に整理(簡単化)することができる。
カルノー図上でマスが隣り合う場合は、変化している論理変数を消去した残りの変数で表示可能になる。
2.カルノー図を用いた論理式の簡単化
以下のようなカルノー図があったとします。
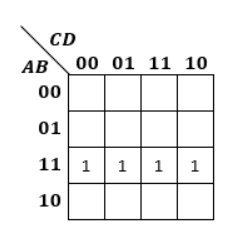
このカルノー図を表す論理式をXとすると、Xは以下のようになります。
X=ABCD+ABCD+ABCD+ABCD
ですが、よくよく考えるとこの論理式はABが固定でCとDの全組み合わせがそれにくっついている形になっているので、以下のように表すことができます。
X=AB
このように、論理式は場合によっては簡単化が可能です。
では、以下の用なカルノー図ではどうでしょうか?
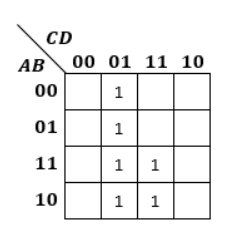
X=ABCD+ABCD+ABCD+ABCD+ABCD+ABCD
そのまま書くとこんな感じになります。
ごちゃごちゃしていて見づらいですね。
ですが、この論理式を簡単化すると以下のようになります。
X=CD+AD
簡単化するとこんなスッキリするのです。
ということで、やり方の説明に移ります。
方法は簡単で、カルノー図上で“1”が隣り合うマスに注目していくだけです。
先程の例をそのまま使用して考えていきます。
まず、”1″が隣り合うマスに目印を付けます。
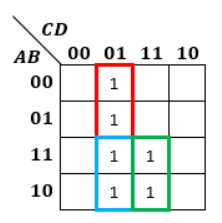
囲み方は他にも存在しますが、今はこの囲みで考えていきます。
赤枠に注目してください。
この部分の論理式はABCD+ABCDですよね?
分配則により、A・(B+C)=(A・B)+(A・C)という関係が成り立つので、ABCD+ABCD=ACD(B+B)になります。
B+B=1なので、赤枠部分はACDということになります。
つまり、マスが隣り合う場合は変化している論理変数を消去した残りの変数で表示可能なのです。
Bが“0”だった場合、Bは“1”になります。
逆に、Bが“1”だった場合、Bは“0”になります。
B+BはBとBの論理和なので、「BまたはB」を表している。
つまり、Bが“0”だろうが“1”だろうがB+Bは必ず“1”になる。
同様に考えていくと、青枠及び緑枠は以下のようになります。
ABCD+ABCD ⇒ ACD
ABCD+ABCD ⇒ ACD
なので、論理式はACD+ACD+ACDと簡単化できます。
ただ、ここにまた分配則を適用すると、ACD+ACD=CD、ACD+ACD=ADになることがわかると思います。
つまり、まだ簡単化の余地があるんですね。
ではどう考えれば良いのかと言うと、“1”が隣り合う(2つ並んだ)マスだけではなく、4つ並んだマス、8つ並んだマスがないかにも注目してみましょう。
“1”が偶数個並んだマスを探そうということです。
改めて“1”が偶数個並んだマスに目印を付けてみます。
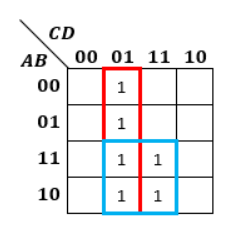
赤枠と青枠で一部被っている箇所がありますが、問題ありません。
どちらにも含まれるものが存在するだけですから。
また赤枠に注目してみましょう。
この部分の論理式はABCD+ABCD+ABCD+ABCDです。
分配則を適用すると、ACD(B+B)+ACD(B+B)=ACD+ACD=CD(A+A)=CDとなります。
つまり、マスが隣り合う場合は変化している論理変数を消去した残りの変数で表示可能という関係が、4つ並んだマスに対しても適用されるのです。
ここでは説明しませんが、8つ並んでも同じように分配則を使えば簡単化されます。
同様に考えていくと、青枠内で変化していないのはADなので、青枠の論理式はADになります。
よって、このカルノー図はX=CD+ADと論理式で表すことができるわけです。
これがカルノー図を用いた簡単化です。
ちなみに、隣り合うマスに注目すると言いましたが、厳密には論理変数が1つだけ変化している組み合わせに注目するです。
その為、以下のような配置でも簡単化が可能です。(論理式:BD)
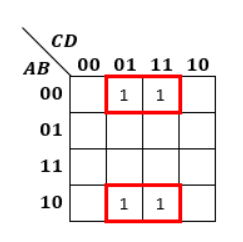
[00]⇒[01]⇒[11]⇒[10]⇒[00]と一巡するので、当たり前と言えば当たり前ですけど、結構言われないと気付かなかったりします。
以上、「カルノー図を用いた論理式の簡単化」についての説明でした。




