今回は、「関数と逆関数の関係」についての説明です。
目次
1.初めに
学校で数学を学んでいた時に、一次関数や二次関数について習ったかと思います。
社会に出ると知識としては役に立たないことが多い気もする数学ですが、一次関数に関しては日常的に使用する機会がありますので、ちゃんと理解しておきたいところです。
ところで、関数って何か答えられますか?
一次関数と二次関数について理解していても、この問いに答えられる方は少ないのではないでしょうか?
何故なら、一次関数や二次関数が何なのか知っていれば、別に関数とは何なのか知らなくても困らないからです。
でも、こういうのってふと気になることがあるんですよね。
ということで、今回は関数とは何なのか、逆関数とは何なのか、という部分に焦点を当てていこうと思います。
2.関数とは?
関数[function]とは、2つの変数で式を構成された変数に応じてもう片方の変数が変化するようになっている関係式のことです。
xとyという変数があった時、xが決まるとyも決まる関係だということです。
例えば、1個100円のりんごがあったとします。
ここで、りんごの個数をx、値段の合計をyとおくと、y=100xという式が成り立ちますよね?
りんごを2個買った場合はxに2を代入することで、y=100×2=200円だと求めることができるわけです。
変数xを指定したら、変数yの値も決定したでしょう?
この関係を満たしている式が関数なのです。
3.逆関数とは?
逆関数[inverse function]とは、変数の役割を反転させた関数のことです。
具体例を見ながら説明していきますね。
先程も出てきたy=2xの逆関数を考えます。
y=2xという関数は、「ある数xに2を掛けた数yを作る」という式を表しています。
この役割が反転すると、「ある数xを2で割った数yを作る」になりますよね?
その為、y=2xの逆関数はy=x/2になります。
これが役割を反転させるという意味です。
逆関数の求め方はもう一つありますが、それは後程説明します。
4.足し算/引き算と掛け算/割り算が入り混じった場合の逆関数
足し算/引き算だけか掛け算/割り算だけの関数の逆関数はわかりやすいのですが、足し算/引き算と掛け算/割り算が入り混じる関数の逆関数を求める際は注意が必要になります。
試しに、関数y=2x+1の逆関数を求めてみます。
この関数の役割は、「ある数xに2を掛けた後、1を足した数yを作る」です。
これに対して逆数は、「ある数xから1を引いた後、2で割った数yを作る」になります。
何かに気が付きませんか?
そう、計算する順番も反転しているんですよ。
「ある数xを2で割った後、1を引いた数yを作る」だと間違いなんです。
実際、y=2x+1の逆数はy=(x-1)/2になります。
後者で求めてしまうと、y=x/2-1になるので試しに計算してみると違いがわかるはずです。
この点は注意が必要です。
5.逆関数を簡単に求める方法
逆関数の考え方が若干間違えやすいですが、ある方法で逆関数を求めれば特にそこを気にする必要は無くなります。
その方法とは、変数の役割を反転させることです。
つまり、y=2x+1という関数があるのなら、xとyを入れ替えたx=2y+1が逆関数なんです。
式を整理すると確かに逆関数になっていることがわかります。
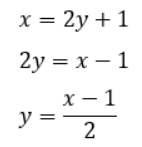
もしも逆関数を求める必要があった場合、この方法を使えば簡単に求めることができるのです。
6.逆関数はy=xを基準として対称になる
逆関数には、y=xを基準として対称になるという性質があります。
y=2x+1の逆関数はy=(x-1)/2でしたよね?
試しに本当にそうなっているのか見てみましょう。
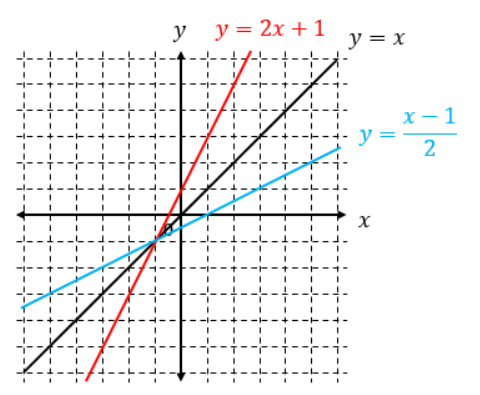
(-1,-1)の地点で交わって、y=xを基準に対称になっているのが見て取れますね。
7.逆関数は存在しない場合もある
逆関数は変数に応じてもう一つの変数がただ一つに決まる関数に対してのみ存在します。
なので、一次関数や指数・対数などには逆関数が存在するのですが、二次関数などには存在しません。
例えば、y=x2という関数があった場合、y=9になるxは3と-3の2種類存在します。
このような場合は、逆関数が無いのです。
8.結局のところ逆関数は何に使うのか?
逆関数の求め方や性質は理解できたかと思います。
ただ、『逆関数って何に使うの?』という疑問は残りますよね?
一次関数とか二次関数は日常で使うことがありますし、指数は自然界に存在します。
では、逆関数って何なんだ、と。
端的に言うと、ある変換方式(関数)に対して元に戻すための逆変換方式(逆関数)を求めています。
関数は、ある数を別の数に変換しているものですよね?
y=2x+1という関数がやっていることを図で表すと、以下のようになります。
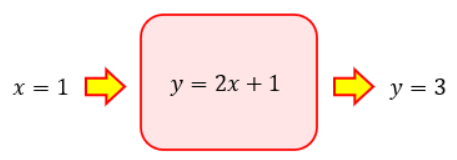
y=2x+1という変換ボックスがあり、xを入力すると変換されてyが出力されるわけです。
逆関数は、この変換された数を入力すれば変換前の状態に戻すことができる関数になっています。
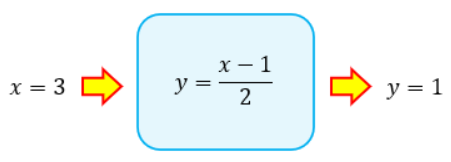
つまり、何かしらの変換を数式で表すことができたのなら、元に戻す方法も逆関数で求めることができるんです。
イメージとしては、発電機に対する電動機、暗号化に対する復号です。
実際にどう応用されているかはその道のプロにしかわかりませんけどね。
以上、「関数と逆関数の関係」についての説明でした。



