今回は、「R-C回路のコンデンサ端子電圧の時間的変化(例題)」についての説明です。
1.初めに
R-C回路のコンデンサ端子電圧/端子電流の時間的変化の原理を過去にまとめてきたので、今回は実際に例題を解いていこうと思います。
そうしないと記憶に定着しないですからね。


前提としてR-C回路の過渡現象について知っている必要があります。
ある状態から時間経過に従って変化し、一定時間経過後に一定値に収まる(定常状態になる)現象のことを過渡現象と呼びます。
逆に言うと、一定時間経過するまでは変化します。
この説明でよくわからないという場合は以下の記事を先にご覧ください。

2.R-C回路のコンデンサ端子電圧の時間的変化(充電過程)の例題
図1のような単純なR-C回路について考えると、コンデンサの端子電圧VCは以下の公式に従って変化します。
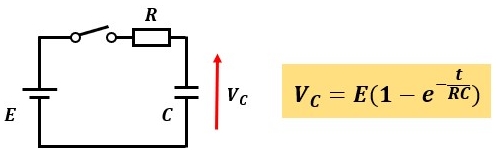
図1のR-C回路にて、1[s]間スイッチをONした時のコンデンサに蓄えられる電荷Q[C]をこの関係式を用いて試しに求めてみましょう。
E=9[V]、R=1[kΩ]、C=1[μF]とします。
全て公式に代入すると、VC=9(1-e-1000)≒9[V]になります。
※ e≒2.7で-1000乗なのでほぼ0として扱っています。
電荷Q[C]・静電容量C[F]・電圧V[V]の関係はQ=CVなので、コンデンサに蓄えられる電荷Q=(1×10-6)×9=9[μC]となります。
ちなみに、時定数Tを求めると、T=RC=1[ms]となります。
なので、少なくともフルチャージの63%までは1[ms]で充電されることがわかります。
その為、1[s]もあればこのコンデンサはフルチャージされると想像できるので、最初からQ=CV(Vは電源電圧Eに値する)の関係で電荷を求めても同じ解になります。
3.R-C回路のコンデンサ端子電圧の時間的変化(充電過程)の例題 複雑Ver.
公式を覚えていればR-C回路のコンデンサ端子電圧が時間経過によりどう変化するかわかりますが、回路が一見複雑になると途端に訳が分からなくなるかもしれません。(体験談)
なので、ちょっと複雑な回路についても考えてみましょう。
こうしてまとめれば少なくとも私の記憶には解法の印象が残りますからね。
では、図2のコンデンサ端子電圧について考えてみます。
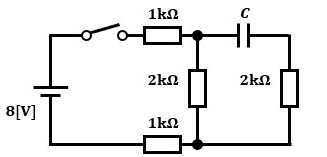
コンデンサの端子電圧の時間的変化はR-C回路におけるものでしたよね?
図2のように抵抗が複数ある場合はどう考えれば良いと思いますか?
答えは単純で、“R-C回路にしてしまえばいい”です。
ということで、コンデンサを基準にテブナンの定理を使用して回路を簡略化しましょう。
テブナンの定理についての説明は別ページで行っているので、簡単な導き方だけ以下に記載します。
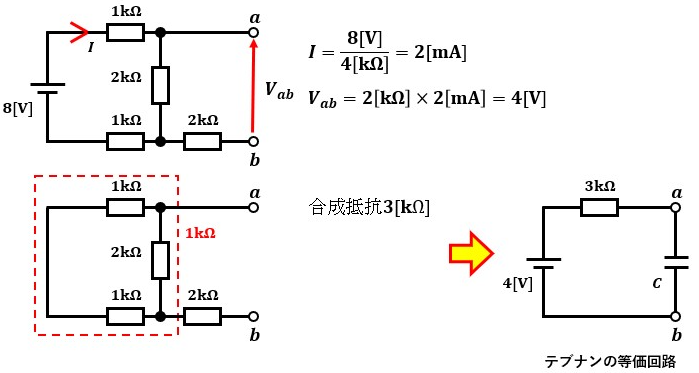
こうすることで最も単純なR-C回路で表示することができたので、後はコンデンサの静電容量Cと経過時間によってコンデンサ端子電圧が導き出せます。
以上、「R-C回路のコンデンサ端子電圧の時間的変化(例題)」についての説明でした。



