今回は、「V結線回路の練習問題」についての説明です。
1.本記事で出てくる公式や考え方のまとめページリンク
2.V結線回路の練習問題①
電験三種の過去問に出てきたV結線回路の問題が初見では大分混乱したので、今回は考え方をまとめておこうと思って記事を書いています。
図1のようにV結線電源に抵抗R[Ω]とインダクタンスL[H]のコイルからなる三相平衡負荷が繋がっています。
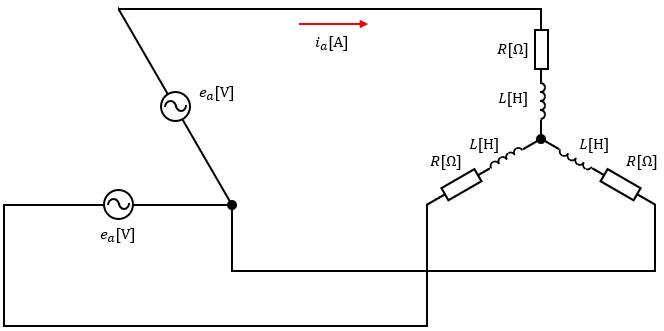
ある時間t[s]における線間電圧eaは√2Vsinωt[V]、ebはeaに対して振幅が等しく、位相が120°遅れていたとします。
電源の内部インピーダンスは考えないものとした時、三相電力Pの値を求めてみましょう。
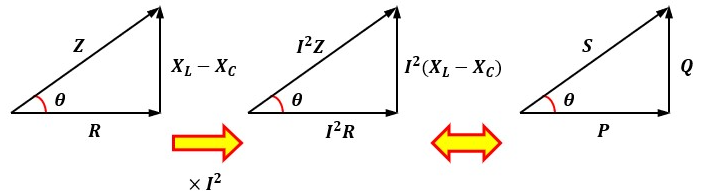
まず、交流回路の電力について考える場合、基本思考として『インピーダンスの三角形を描く』と覚えましょう。
単相交流だろうが三相交流だろうがここは変わりません。
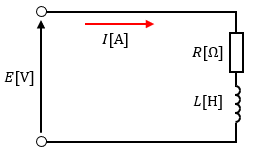
ただ、三相交流の場合は一相の電力を考えた後に3倍することで三相電力が求まるので、図2のように一相分を抜き出す必要があります。
最初に電源Eについて考えます。
文面でも述べていますが、ea及びebは相電圧ではなく線間電圧になっていますので、相電圧に変換する必要があります。
まあ、V結線の相電圧と線電圧って同じですけどね。
また、eaは瞬時値表示で、振幅である√6Vとは最大値のことなので、実効値に変換する必要があります。
よって、一相を取り出した時の電源Eは√6V÷√3÷√2=Vとなります。
次に、相電流を求めます。
一相分の回路について考えると、電源V[V]のR-L直列回路になっていることがわかっています。
なので、インピーダンスの三角形を描いて、回路全体に流れる電流I[A]を求めます。
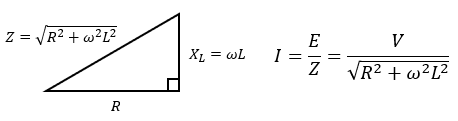
後は電力を求めるだけなのですが、個人的に地味に悩むポイントがあります。
『三相電力Pって有効電力?皮相電力?』という点です。
実際の問題でも、今解いている練習問題のように特に記載がない場合が普通にあります。
基本的に注記がない場合は有効電力のことを指していると覚えておきましょう。
こんなところでミスしたくないのなら。
ということで、インピーダンスの三角形を描いた時の抵抗成分にI2を掛けて三相分の有効電力を求めましょう。
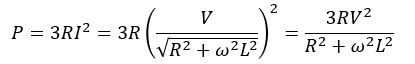
これで三相電力Pを求めることができました。
「瞬時値表示は実効値に直す」・「ただ単に電力を求めるように書かれていたら有効電力を求める」という2点で引っかけてくる問題は多いので、注意しましょうね。
3.V結線回路の練習問題②
図1の回路に静電容量C[F]のコンデンサを付け足して図5のようにしました。
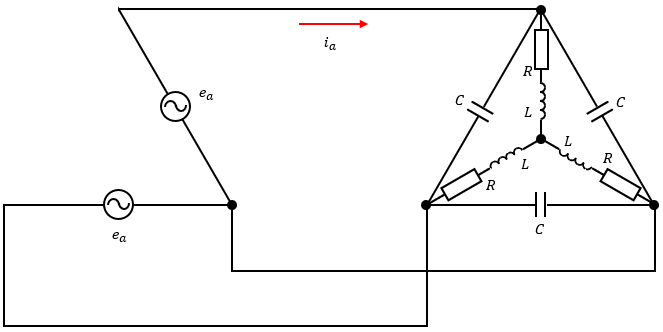
この時、iaの波形はeaの波形に対して位相が30°遅れていました。
この時の静電容量C[F]の値を求めてみましょう。
何やら位相差が条件に出てきたので、電圧と電流のベクトル図を描いてみましょう。
それに当たり、V-Δ結線回路の電圧と電流を図6のように置きます。
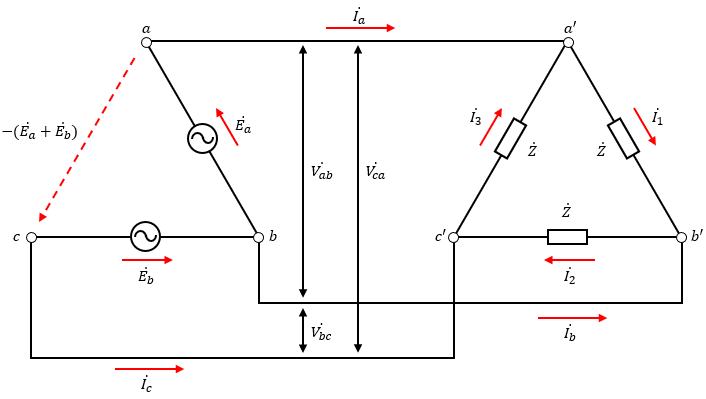
まずは、電圧のベクトル図について考えてみます。
Eaを基準とした時、電圧のベクトル図は図7のようになります。
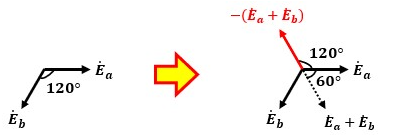
Δ結線における線間電圧と相電圧は等しいので、Ea=Vab、Eb=Vbc、-(Ea+Eb)=Vcaになっています。
ここまではV結線回路の復習です。
次に、電流のベクトル図について考えてみます。
Ia=I1-I3、Ib=I2-I1、Ic=I3-I2なので、I1を基準として相電流と線電流のベクトル図を描くと図8のようになります。。
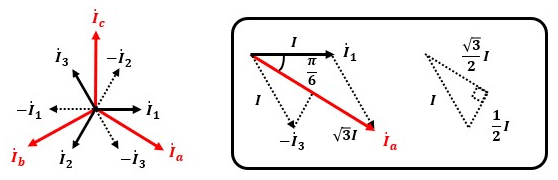
つまり、線電流に対して相電流は30°進んでいます。
図6における線電流Iaは図5におけるiaのことです。
最初の条件を思い出してください。
「iaの波形はeaの波形に対して位相が30°遅れる」とされていましたよね?
つまり、線間電圧eaに対して線電流iaは30°遅れています。
では、相電圧と相電流の位相差はどうなっているでしょうか?
- 線間電圧と相電圧の位相は同じ。
- 線間電圧に対して線電流は30°遅れる。
- 線電流に対して相電流は30°進む。
以上の条件を踏まえると、相電圧と相電流の位相は同じであることがわかります。
つまり、一相分を抜き出した回路におけるインピーダンスZのリアクタンス部分(コイルの誘導性リアクタンスXL及びコンデンサの容量性リアクタンスXC)は、打ち消し合って“0”になっていることがわかります。
なので、合成インピーダンスを求めて、虚数部分を“0”とすることで静電容量Cを計算しましょう。
まず、相電圧と相電流の位相が同じになるのはV-Δ結線回路の時なので、負荷側をΔ結線に変換する必要があります。
三相平衡負荷のY-Δ変換時はインピーダンスを3倍にすれば良いので、3R+3XLとXCが並列接続されている回路とみなすことができます。
そこで、一相分の回路を抜き出すと図9のようになります。
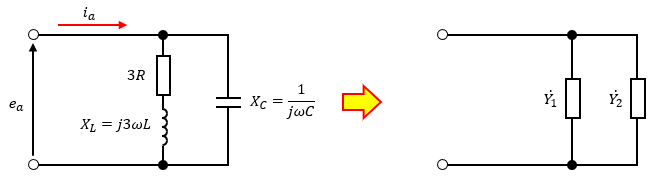
並列接続になっているので、合成アドミタンスを求めていきます。
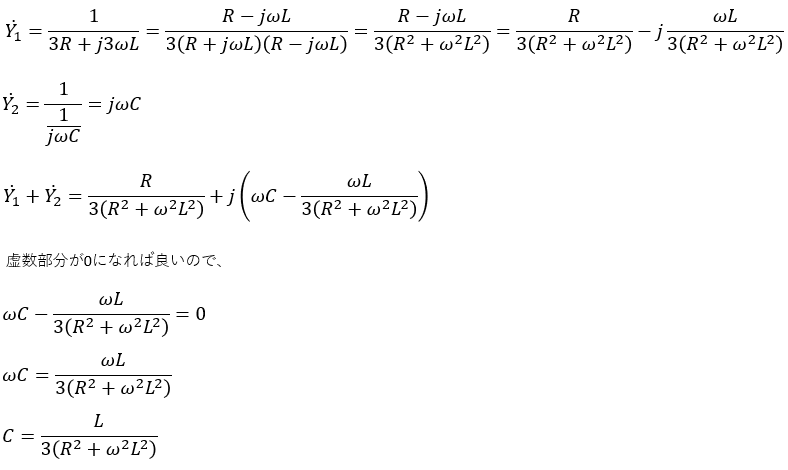
これで静電容量Cが求まりました。
大体意味深な条件が足されると、計算がしやすいようになっているものです。
さて、ここまで解いてみてあることを忘れているのではないでしょうか?
この練習問題、電源がV結線になっているんですよね。
ですが、問題を解く上でV結線であることが関係してくることは無かったです。
つまり、計算する上でV結線であることが影響してくることはあまり無いのです。
影響があるとしたら、電源の利用率が全電源容量の86.6%までになる点に関する問題くらいかと思われます。
V結線回路になったからといってあまり複雑に考えないようにしましょうね。
以上、「V結線回路の練習問題」についての説明でした。