今回は、「R-C回路のコンデンサ端子電圧/電流の時間的変化(放電過程)」についての説明です。
1.ポイント
2.初めに
コンデンサには、電荷を蓄えたり放出したりできるという特徴がありました。
その為、コンデンサの端子電流及び端子電圧は時間的変化をします。
こうして時間的変化をし、一定時間経過後に一定値に収まる(定常状態になる)現象のことを過渡現象と言い、その変化の度合いを表しているのが時定数でした。
ここまではこれまで説明してきた内容です。
直接このページへアクセスした方の中にはその辺りの知識が不足している方もいるかもしれないので、自信が無い方は以下の記事にも目を通しておくことを推奨します。
今回は、R-C回路の放電過程のコンデンサ端子電流の時間的変化を表す式を求めていこうと思います。
ちなみに、符号の向きに関しては電圧の向き・電流の向きを置く方向によって変化するので、他のサイトと異なっている可能性はあります。
方向を合わせれば同じになるはずですけどね。
3.R-C回路のコンデンサ端子電圧の時間的変化(放電過程)
図1左のようにR-C回路を形成して起電力E[V]の電源で充電し、充分に時間が経過したところで図1右のようにスイッチSを切り替えたとします。
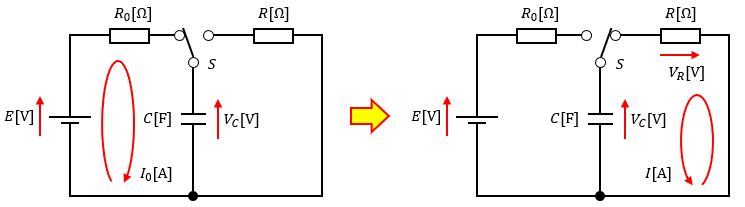
このスイッチSを切り替えた瞬間をt=0[s]とし、コンデンサはフル充電されているものとします。
ある時間t[s]におけるコンデンサに蓄えられた電荷をQ(t)、コンデンサの端子電圧をVC(t)、回路を流れる電流をI(t)、抵抗の端子電圧をVR(t)とします。
※ 以降の計算で(t)を付けていくと見た目がすごいことになってわかりづらかったので、それぞれQ、VC、I、VRと表示します。脳内補完してください。
単位時間当たりの電荷の変化量が電流なので、I=dQ/dtです。
ここにQ=CVの関係を適用すると、I=CdVC/dtになります。
R-C回路を流れる電流は直列なので一定です。
なので、VR=R×CdVC/dtになります。
よって、0=VC+VR=VC+RCdVC/dtと表せます。
この微分方程式を整理してVCを求めていきます。
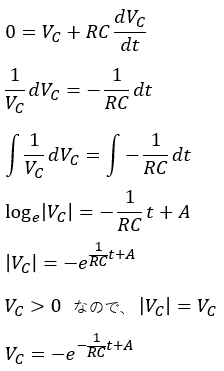
コンデンサはフル充電されているものとしていたので、t=0[s]の時のコンデンサ端子電圧VC(t)はE[V]です。
この関係を先程の式に代入すると以下のようになります。
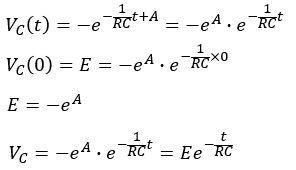
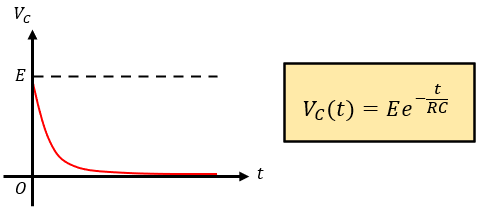
これでR-C回路の放電過程のコンデンサ端子電圧の時間的変化を表す式が求まりました。
ちなみに、放電してから充分に時間が経つという条件は、この式のtを無限大に大きくすることに等しいです。
なので、指数部分が0に近づき、VCは最終的に0に近づくことがわかります。
この関係を図示すると、図2のようなよく見かけるグラフを描くのです。

4.R-C回路のコンデンサ端子電流の時間的変化(放電過程)
コンデンサ端子電圧を求めたので、これを利用してコンデンサに流れる電流(回路に流れる電流)を求めます。
まず、Q=CVなので、Q(t)=CVC(t)になります。
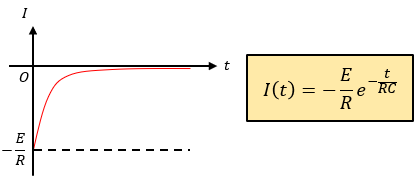
I=dQ/dtなので、I(t)=dCVC(t)/dtとなり、この式を時間で微分すればI(t)が求まります。
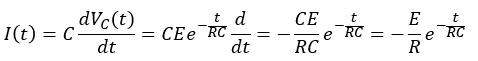
t=0[s]の時の電流はーE/Rになるので、この関係を図示すると図3のようになります。

余談ですが、コンデンサ端子電圧の時間的変化を表す式にt=RC(時定数)を代入すると、0.632Eになります。
最終値の63.2%に達するまでにかかる時間のことを時定数と呼んでいましたが、時定数の条件付けはこうして行われていたのですよ。
以上、「R-C回路のコンデンサ端子電圧/電流の時間的変化(放電過程)」についての説明でした。





