【基礎から学ぶ電気回路】 三相交流の瞬時値表示とベクトル表示

今回は、「三相交流の瞬時値表示とベクトル表示」についての説明です。

１．三相交流回路の構成と波形

3つの単相交流回路を組み合わせてできたものが三相交流回路です。

三相交流回路を構成する3つの単相交流起電力をe_a、e_b、e_cとすると、各瞬間起電力の波形は以下のように表せます。

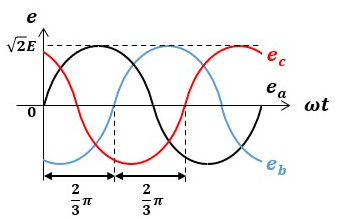
見てわかる通り、2π/3(120°)ずつ位相差のある単相交流3つにて構成されています。

では、実際にどう回路を構成するのかというと、図2のような形になります。

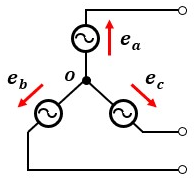
点Oに当たる位置をグランド(基準点)として、各端子から起電力を供給する仕組みです。

２．三相交流の瞬時値表示とベクトル表示

図1の三相交流回路を構成する起電力の瞬時値表示は以下のようになっています。

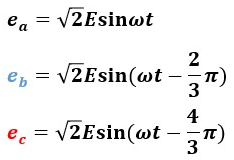
この瞬時値表示をベクトル表示に切り替えると以下のように表せます。

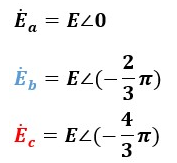
√2があったり無かったりするのは実効値のお話なので、そこから説明が必要な場合は三相交流の前に交流回路の記事からざっと目を通すことをおすすめします。

【基礎から学ぶ電気回路】 正弦波交流とは？負方向の電圧とはどういう意味なのか？

電気回路に流れる電気信号は、直流と交流に二分されます。直流は基本的に一定値として取り扱うので比較的理解しやすいのですが、交流になると正弦波状に変化するせいでちょっとわかりづらくなってきます。なるべく初心者の方でもわかりやすいよう噛み砕いて説明をしていきますので、腰を据えて読んでみてください。今回は正弦波交流についてです。

www.elmusicwisdom.site

2022.05.28

ベクトル表示からベクトル図を描くと以下のようになります。

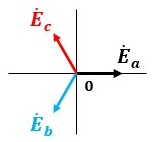
E・_aを基準として120°と240°(－120°)位相が異なるのがE・_b及びE・_cなので、E・_bとE・_cは横軸を基点として上下対象になっていることがわかりますね。
これらを座標表示すると、E・_aは(E,0)、E・_bは(－E/2,－√3E/2)、E・_cは(－E/2,√3E/2)になります。
この3つの座標のX軸とY軸の値を足し合わせてみると(0,0)になります。

つまり、E・_a＋E・_b＋E・_cという3つのベクトルのベクトル和は必ず0になるようになっています。

よって、ベクトル表示する前の瞬時値の状態でも同様のことが言え、e_a＋e_b＋e_c=0も成り立ちます。

その為、「そもそも三相交流とは何なのか」の説明でも述べましたが、瞬時値電流も総和が0になり、帰路を1つにまとめるとその電線には電流が流れなくなるのです。

以上のような理由から、図2の点Oはグランドに当たるはずなのにグランドの記号が描かれていないという状態がよく見られるのです。
※ 描かれている場合もありますが、大抵省略されています。

３．対称三相交流とは？

一般的な三相交流と言ったらここで説明したような三相交流を指しています。
有する特徴は以下の通りです。

この条件を満たしている三相交流のことを対称三相交流と言います。
なので、ただ単に三相交流だと言っていたら『多分対称三相交流のことなんだろうな』と思ってください。

ちなみに、対象三相交流の条件に負荷は関係してきません。
別物の負荷が繋がっていようが、上記の条件を満たしていれば対象三相交流です。

以上、「三相交流の瞬時値表示とベクトル表示」についての説明でした。

---