今回は、「オイラーの公式」についての説明です。
1.初めに
インターネットで交流回路について学んでいると、何の脈拍もなく指数関数と三角関数で相互に変換してくることがあります。
この変換にはオイラーの公式というものを用いるのですが、何でかはわかりませんが「オイラーの公式に則った」という旨が大概書かれていません。
おそらくですが、参考書などの内容をそのままコピペしたりしているので、それをまとめた人がしっかりと理解していないのではないかと思います。
そんなWebページに限って、とりあえず色々書くだけ書いて結局何が言いたいのかわからないことが多いですからね…。
今回は、オイラーの公式とはどんなものなのかを解説していきます。
2.オイラーの公式とは?
オイラーの公式とは、先程述べたように指数関数と三角関数の間に成り立っている特殊な関係のことを指しています。
実際に成り立っている関係は、以下の通りです。
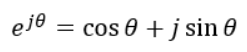
指数関数(ネイピア数eのべき乗)と三角関数がイコールになっていますね。
数学が嫌いな人は見ているだけで頭が痛くなりそうな公式ですね。
この形のままだとわかりづらい関係式でしかないので、実際に数値を当て嵌めて考えてみましょう。
ということで、角度θ=0,π/2,π,3/2πの場合について考えてみると、以下のようになります。
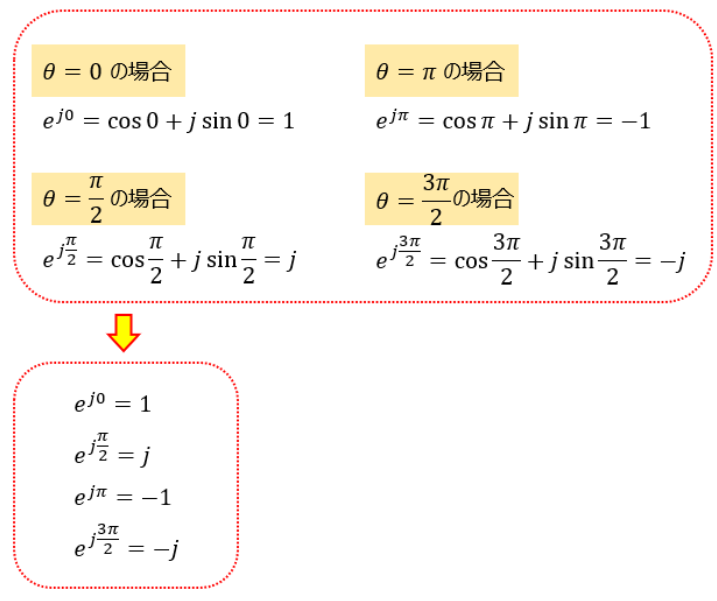
こんな関係を表しているのがオイラーの公式なのです。
オイラーの公式にはもちろん導き方があるのですが、マクローリン展開とか出てきて混乱を生みそうなので割愛します。
うまく簡潔にまとめられそうなら後で追記しますよ。
3.オイラーの公式を用いた例題
数学以外にも言えますが、とりあえず練習問題・例題を解くのが一番なので、実際に変換しながら関係を確認してみましょう。
以下のような複素数があったとします。
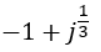
虚数項が何を意味しているのか読み取りづらいですね。
この複素数を極座標表示にしてみましょう。
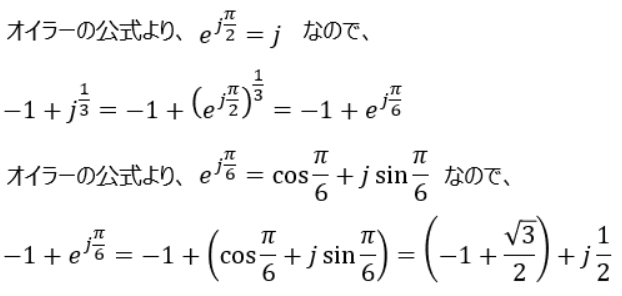
後は極座標表示に必要なパラメータを求めるだけです。

4.オイラーの等式とは?
オイラーの公式と似た名称のものとして、オイラーの等式があります。
同じものを指しているわけではありません。
関連はありますが、別物です。
オイラーの等式とは、以下のような関係式を指しています。
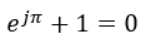
やけにサッパリとした式ですよね。
求め方は簡単で、オイラーの公式にて角度を円周率πにするだけです。
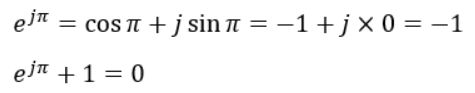
オイラーの等式は、数学史上最も美しい等式だと言われています。
何故かと言うと、ネイピア数eと虚数jと円周率πはそれぞれ別の人が定義したものだからです。
推理ゲームでは、別々の人の証言をかき集めて一つの真実への結びつけますよね?
伏線を散りばめて回収することで真相が見えてくるのです。
これと同じようなことを現実で意図せず引き起こしたわけです。
最も美しいと言われているのも納得ですね。
5.オイラーの公式から加法定理を導き出せる
三角関数には加法定理というものが存在します。
実はこの加法定理ですが、オイラーの公式を使って導き出すことが可能です。
せっかくなのでそちらの解法も記載しておきますね。

以上、「オイラーの公式」についての説明でした。


