今回は、「磁気に関するクーロンの法則」についての説明です。
1.磁気に関するクーロンの法則
「静電気に関するクーロンの法則」と併せて考えると覚えやすいです。
点とみなせるほど小さな磁極のことを点磁極と呼びます。
そういう概念として認識しましょう。
2つの点磁極に働く磁力(反発力・吸引力)の大きさF[N]は、2つの磁極の強さm1とm2の積に比例し、距離の2乗に反比例します。
この関係を、磁気に関するクーロンの法則と呼び、磁力のことを磁気力とも呼びます。
磁極の強さの量記号はm、単位は[Wb]です。
仮に真空中にm1[Wb](N極/正極)とm2[Wb](S極/負極)の点磁極が存在していた場合、図1のように磁力(ここでは正と負の異種磁極が存在している為、吸引力が発生)が働きます。
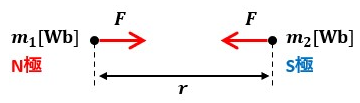
式で表すと以下のようになります。
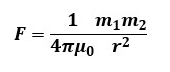
rは距離で、単位は[m]です。
μ0は真空中の透磁率で、単位は[H/m]です。
μは「ミュー」と読みます。
透磁率とは、媒質(空気などの物質が存在できる場所)での磁束の通しやすさを表す定数です。
磁束を透過する割合だから透磁率ということですね。
※ 磁束に関しては次の記事で説明します。
磁極が真空中に存在している場合、1/4πμ0の値は以下のようになります。
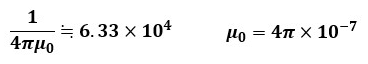
真空以外の媒質では透磁率μを用い、透磁率μが真空中の透磁率μ0の何倍かを表した比のことを比透磁率μsと呼びます。
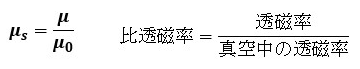
以上の点を踏まえて磁力の式を整理すると、次のように表すこともできます。
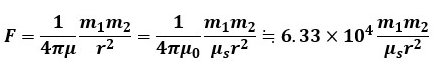
真空中の比透磁率μsは、μ=μ0となる関係からμs=1として計算することになります。
以上、「磁気に関するクーロンの法則」についての説明でした。




