今回は、「自己インダクタンスと相互インダクタンス」についての説明です。
1.ポイント
何れもコイルの巻数に比例し、磁気抵抗に反比例する。
自己インダクタンス:コイルの巻数の2乗÷磁気抵抗
相互インダクタンス:コイルの巻数×もう一方のコイルの巻数÷磁気抵抗
電磁結合している結合回路でコイルに磁束が鎖交する割合。
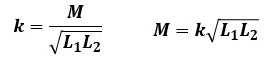
直列接続されている自己インダクタンスを足し合わせ、磁束の方向により相互インダクタンスの2倍の値を足した/引いた値が合成インダクタンスになる。
2.自己インダクタンスと相互インダクタンス
図1のように2つのコイルが隣り合っています。
両コイルは電磁結合している結合回路です。
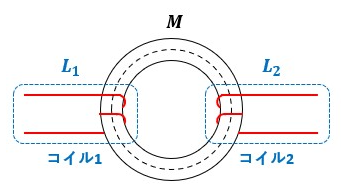
コイル1の巻数はN1[回]、コイル1の自己インダクタンスはL1[H]、コイル2の巻数はN2[回]、コイル2の自己インダクタンスはL2[H]、相互インダクタンスはM[H]です。
環状コイルの自己インダクタンスはコイルの巻数N[回]の2乗に比例し、磁気抵抗Rm[A/Wb]に反比例する為、以下のようになります。
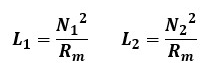
相互インダクタンスは以下のように表せた為、式を変形していきます。
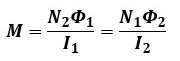

※ N1Φ2/I2を式変形しても同様の結果になります。
つまり、自己インダクタンスも相互インダクタンスもコイルの巻数に比例し、磁気抵抗に反比例するという関係は同じということがわかります。
3.結合係数
電磁結合している結合回路の結合の程度を表す結合係数kというものがあります。
厳密には、磁束が鎖交する割合を示しています。
図2のようにコイル1に電流I1[A]が流れて磁束Φ1[Wb]が発生しているとします。
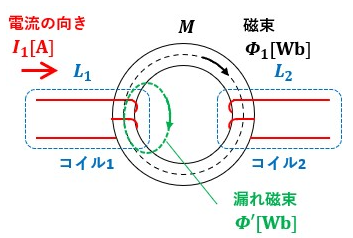
これまでの説明では、コイル1に電流I1[A]が流れることにより磁束Φ1[Wb]が発生し、発生した磁束Φ1[Wb]が全てコイル2と鎖交する場合について考えていましたが、実際は緑線で示しているようなコイル2と鎖交しない磁束Φ'[Wb]が発生していることがあります。
この磁束のことを漏れ磁束と呼びます。
結合係数kは、どの程度漏れ磁束が発生しているか、つまり磁束がどれだけ鎖交しているかを表しているということです。
結合係数kの範囲は0≦k≦1で、k=1の時は漏れ磁束が無いということになります。
※ 実際は漏れ磁束が少なからずあるので1より小さくなります。
結合係数kは式で表すと以下のようになります。
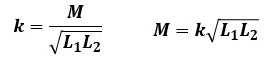
4.インダクタンスを直列接続した場合の合成インダクタンス
図3のように、2つの回路が直列に接続されているとします。
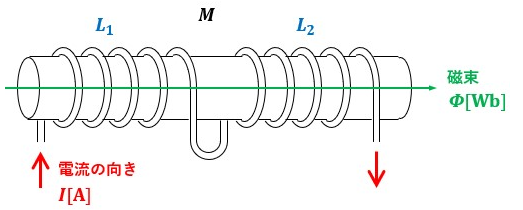
図3の場合、各コイルの磁束の方向が一致しています。(※右ねじの法則より)
この時の合成インダクタンスL0[H]は以下のようになります。
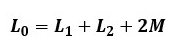
磁束の方向が反対になるようにコイルを直列した場合、相互インダクタンスの符号が-(マイナス)になります。
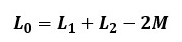
このように、直列接続されている自己インダクタンスを足し合わせ、磁束の方向により相互インダクタンスの2倍の値を足した/引いた値が合成インダクタンスになります。
以上、「自己インダクタンスと相互インダクタンス」についての説明でした。




