今回は、「R-L-C直並列回路の共振」についての説明です。
1.初めに
「交流回路の共振」の説明で、直列共振と並列共振どちらも共振の条件は誘導性リアクタンスXL=容量性リアクタンスXCだと述べました。
これは、単純なR-L-C直列回路/R-L-C並列回路だったからの話です。
今回は、直列と並列が入り混じったR-L-C直並列回路の場合の共振条件について考えていきます。
2.R-L-C直並列回路の直列共振条件
直列共振は、直列回路部分にてインピーダンスの三角形を描いた時にリアクタンス(XLとXC)が打ち消し合って0になるから、XLにかかる電圧VLとXCにかかる電圧VCのベクトル和が0になるというものでした。
つまり、直列共振する条件はインピーダンスのリアクタンスが0になることだと言えます。
なので、図1の回路のインピーダンスを求めてみます。
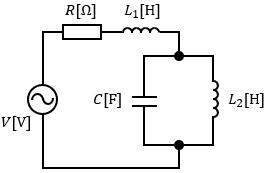
まず、L2とCの並列部分の合成アドミタンスYを求めます。
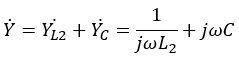
アドミタンスの逆数がインピーダンスなので、回路全体のインピーダンスは以下のようになります。
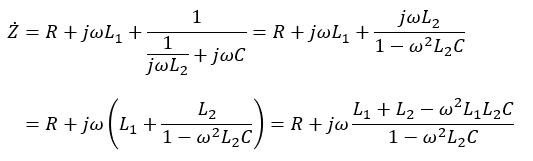
この虚数部分が0になることが直列共振の条件なので、その関係から直列共振する時のωがどうなるか計算してみます。
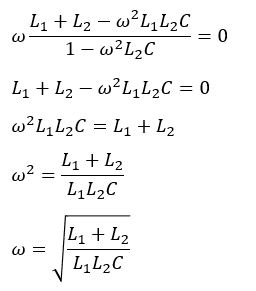
これが図1のR-L-C直並列回路の直列共振条件です。
ちなみに、直列共振すると回路のインピーダンスは実数部分しか残らないので、極めて小さくなると言えます。
3.R-L-C直並列回路の並列共振条件
並列共振は、並列回路部分にて電流の三角形を描いた時にリアクタンス成分に流れる電流(ILとIC)が打ち消し合って0になるから、XLに流れる電流ILとXCに流れる電流ICのベクトル和が0になるというものでした。
つまり、並列共振する条件はL-C並列回路部分のXLとXCが等しくなることだと言えます。
図1の回路の場合、並列接続になっているのはL2とCだけです。
その為、L1は並列共振条件には関係してきません。
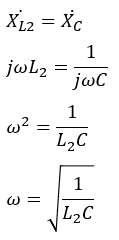
これが図1のR-L-C直並列回路の並列共振条件です。
ちなみに、並列共振すると回路のインピーダンスは極めて大きくなります。
リアクタンスに電流が全く流れなくなるわけですからね。
結局のところ、多少回路が複雑になったところで基本を押さえておけばなんとかなるんですよ。
以上、「R-L-C直並列回路の共振」についての説明でした。




