今回は、「交流回路の共振」についての説明です。
1.ポイント
R-L-C直列回路にて、誘導性リアクタンスXL=容量性リアクタンスXCの時、XLにかかる電圧VLとXCにかかる電圧VCは互いに打ち消し合う。
これを直列共振という。
R-L-C並列回路にて、誘導性リアクタンスXL=容量性リアクタンスXCの時、XLに流れる電流ILとXCに流れる電流ICは互いに打ち消し合う。
これを並列共振という。
交流回路には、共振と呼ばれる状態があります。
R-L-C直列回路とR-L-C並列回路で異なる共振の仕方をする為、それぞれ説明していきます。
2.R-L-C直列回路の共振
まずは、R-L-C直列回路の共振について説明します。
通常、R-L-C直列回路の「インピーダンスの三角形」は図1のようになっています。
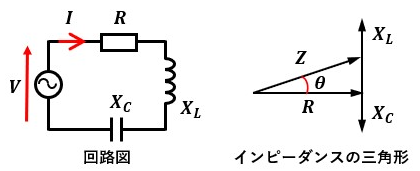
図1では、XL>XCなので上側のベクトル分の方が大きく、このような三角形を描いています。
つまり、誘導性リアクタンスXL=容量性リアクタンスXCの場合、XLとXCが互いに打ち消し合うことでベクトル和が0になることがわかります。
直列回路では電流Iは一定なので、XL=XCの時にXLI=XCIが成り立ちます。
VL=XLI、VC=XCIなので、XLにかかる電圧VLとXCにかかる電圧VCのベクトル和が0になることがわかります。
この状態のことを直列共振と呼びます。
3.R-L-C並列回路の共振
次に、R-L-C並列回路の共振について説明します。
通常、R-L-C並列回路の「電流の三角形」は図2のようになっています。
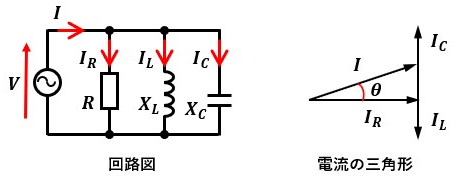
図2では、IC>ILなので上側のベクトル分の方が大きく、このような三角形を描いています。
つまり、誘導性リアクタンスXLに流れる電流IL=容量性リアクタンスXCに流れる電流ICの場合、ILとICが互いに打ち消し合うことでベクトル和が0になることがわかります。
では、ILとICの大きさが等しくなる条件は何でしょう?
並列回路では電圧Vは一定なので、XLIL=XCICが成り立ちます。
ここでXL=XCだとすると、XLIL=XLICとなり、IL=ICとなります。
つまり、XL=XCの時にXLに流れる電流ILとXCに流れる電流ICのベクトル和が0になると言えます。
この状態のことを並列共振と呼びます。
4.共振の条件
以上より、交流回路の共振条件は直列共振・並列共振問わずにXL=XCとなります。
ここで、共振時の周波数をf0、角速度をω0とすると、以下の関係が成り立ちます。
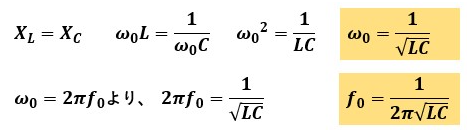
※ ただし、この関係はR-L-C直並列回路になると変化します。
以上、「交流回路の共振」についての説明でした。




