今回は、「ミルマンの定理」についての説明です。
1.ポイント
起電力と抵抗からなる電気回路が複数並列接続されている時に端子電圧を求めることができる。
端子電圧は、「端子間の総電流」を「起電力を短絡除去した時の端子間の合成抵抗の逆数」で割った値となる。
2.ミルマンの定理
ミルマンの定理は全電圧の定理、帆足・ミルマンの定理とも呼ばれます。
図1のような電気回路があります。
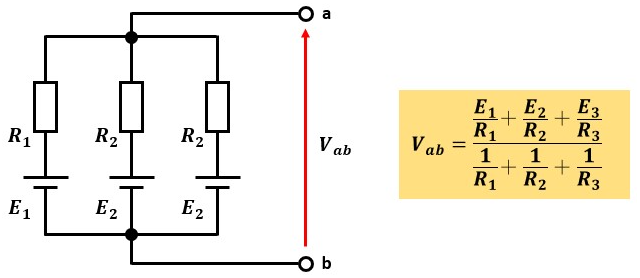
この回路の端子電圧Vabは橙塗り部分のように表せます。
この関係がミルマンの定理です。
端子電圧Vabは、分子がa-b間の総電流、分母が起電力を短絡除去した時のa-b間の合成抵抗の逆数になっています。
つまり、やっていることはオームの法則と変わりはありません。

実際にミルマンの定理を使ってみましょう。
図2のような回路に流れる電流I1、I2、I3を求めてみます。
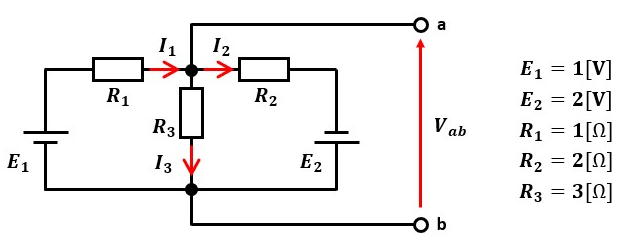
ミルマンの定理に各数値を代入します。
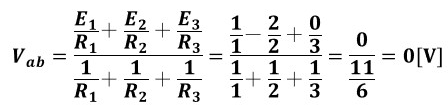
Vab=0[V]であることがわかりました。
ちなみに、計算時の注意点が2つあります。
Vabは、b点を基準の0[V]とした時のa点の電圧を指しています。
上図のE1はVabと同じでb点が基準ですが、E2はVabと違いa点が基準になっています。
その為、Vabと基準が反対になっているE2に関しては、電流の向きが反対です。
つまり、分子のE2/R2にあたる箇所の符号はマイナスになります。
図の回路では、E3にあたる起電力が存在しません。
その為、ミルマンの定理に代入する時は、E3=0[V]という扱いにする必要があります。
話を戻します。
Vab=0[V]なので、各回路を以下のように分けて考えます。
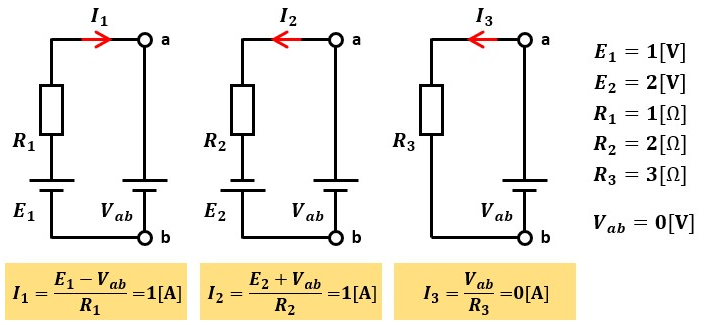
回路に流れる電流I1、I2、I3をミルマンの定理を用いて求めることができました。
ちなみに、「キルヒホッフの法則」、「重ね合わせの理」、「テブナンの定理」でも算出可能なので、併せて理解しておくと便利です。
以上、「ミルマンの定理」についての説明でした。




