今回は、「テブナンの定理とノートンの定理の関係」についての説明です。
1.ポイント
複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電圧源に変換する方法。
この方法で変換した回路を「テブナンの等価回路」と呼ぶ。
複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電流源に変換する方法。
この方法で変換した回路を「ノートンの等価回路」と呼ぶ。
2.テブナンの定理とノートンの定理の関係
複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電圧源に変換する方法がテブナンの定理、複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電流源に変換する方法がノートンの定理でした。
テブナンの定理で回路を整理した結果が図1、ノートンの定理で回路を整理した結果が図2となります。
※ 図1及び図2の左側は同じ回路です。
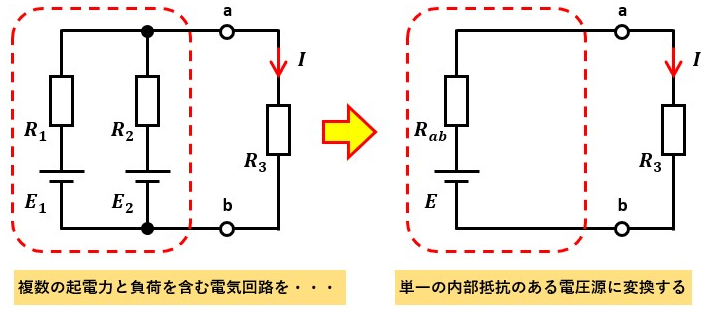
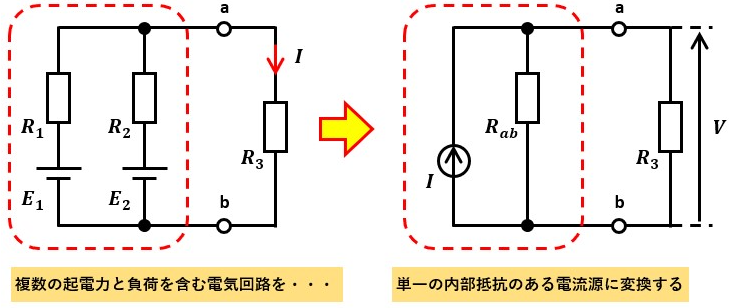
図1と図2を見比べてみればわかるのですが、端子a-b間の右側は抵抗が1つ繋がっているだけで同じ回路になっています。
ということは、赤点線部の回路(テブナンの等価回路/ノートンの等価回路)もイコールになります。
つまり何が言えるかというと、テブナンの等価回路とノートンの等価回路は置換が可能なのです。
3.テブナン等価回路とノートンの等価回路の置換
置換方法は簡単で、内部抵抗Rabはそのままに電圧源と電流源の部分が変化します。
電圧源の起電力Eと電流源の電流Iと内部抵抗Rabの間にはE=Rab×Iという関係が成り立つようになっていて、この関係から置換が可能です。
図3のように同様の回路をテブナンの等価回路とノートンの等価回路で表した例があるので、実際にE=Rab×Iが成り立つのか見てみましょう。
※それぞれの等価回路を導き出す手順はテブナンの定理とノートンの定理の説明にて行っています。
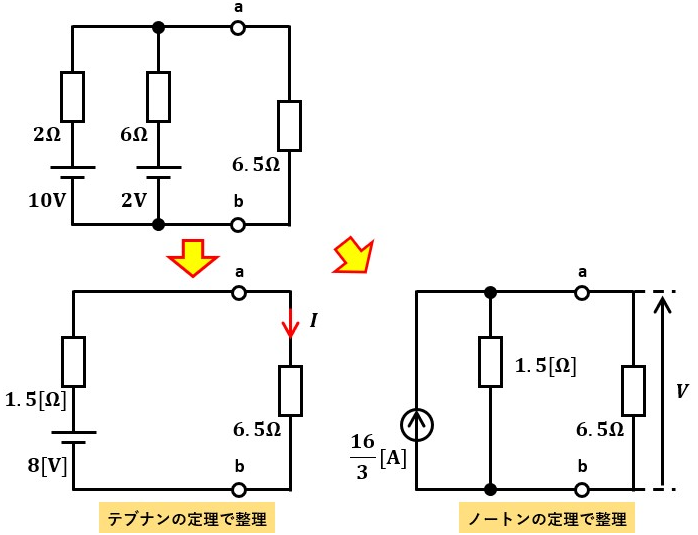
E=Rab×I
8=1.5×16÷3 ⇒ 8=8
E=Rab×Iの関係がしっかり成り立つようになっていますね。
このように、テブナンの等価回路とノートンの等価回路の置換が可能です。
この関係を知っておけば内部抵抗のわかっている電圧源と電流源で互いに置換することが可能になる為、覚えておくと何かと便利です。
何故成り立つのかの証明もあったりするのですが、覚えていてもあまり意味がないので説明は行いませんので悪しからず。
以上、「テブナンの定理とノートンの定理の関係」についての説明でした。




