【基礎から学ぶ電気回路】正弦波交流の平均値・実効値・波高率・波形率の関係

電気回路に流れる電気信号は、直流と交流に二分されます。
直流は基本的に一定値として取り扱うので比較的理解しやすいのですが、交流になると正弦波状に変化するせいでちょっとわかりづらくなってきます。
なるべく初心者の方でもわかりやすいよう噛み砕いて説明をしていきますので、腰を据えて読んでみてください。

今回は、「正弦波交流の平均値・実効値・波高率・波形率の関係」についての説明です。

１．ポイント
２．正弦波交流の平均値
３．正弦波交流の実効値
４．波高率の補足説明

１．ポイント

正弦波交流の平均値

平均値＝(2/π)×最大値

正弦波交流の実効値

実効値＝(1/√2)×最大値

２．正弦波交流の平均値

平均値は、量記号V_a・I_aのように小文字のaが付きます。
aは[average(平均)]のことです。
正弦波交流の平均値とは、波形の1/2周期(山1個分)を平らにならして平均した値のことを指します。

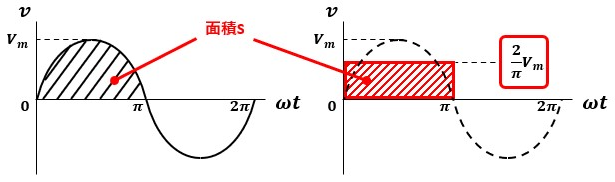
左図の斜線部が波形の1/2周期に該当するので、右図のように平らにして同面積の長方形を作った時の辺の高さが平均値(2/π×V_m)に当たります。
つまり、式で表すと以下のようになります。

３．正弦波交流の実効値

実効値は、量記号V・Iと書きます。
抵抗に交流電圧を与えた際の電力と、同じ抵抗に直流電圧を与えた際の電力が等しくなる時、この交流電圧/電流の実効値は直流電圧/電流と等しくなると定義されています。
簡単に言えば、ある直流電圧/電流と同じ働きをする交流電圧/電流が実効値です。

実効値は、瞬時値を2乗(Square)し、平均(Mean)し、平方根(Root)にした値なので、略してRMSとも呼びます。
順番的にはSMRなのになんでRMSなんでしょうね？

最大値を√2で割った値が実効値に当たるので、式で表すと以下のようになります。

※ 平均値及び実効値が何故このような値になるのか説明すると本筋から大きく外れていくので、次以降の記事で説明します。

ちなみに、交流の波形の表し方に、波高率と波形率というものがあります。

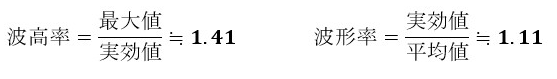
４．波高率の補足説明

波高率とは、波形の最大値(ピーク値)を実効値で割った値のことです。
クレストファクタとも呼びます。

例えば、直流の場合は常に値が一定である為、最大値も実効値も同じ値なので波高率は1となります。
正弦波交流の場合、最大値をV_mとすると実効値はV_m/√2である為、V_m/(V_m√2)=√2≒1.41となります。

図1のように二つので電流波形があったとします。

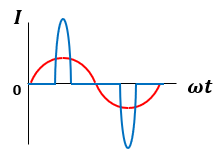
赤い正弦波波形と青い一風変わった交流波形があるわけですが、この二つの交流波形の実効値は同じでした。
実効値は同じだからある直流電圧/電流と同じ働きをするわけですが、この波形が電子部品に供給されることを想像してみてください。
青い波形だけ部品の定格電流を超過することがありそうだと思いませんか？
実際、あり得るのです。
山と谷の部分で瞬時的に定格を超えてしまい、場合によっては規格を満たさなくなる可能性があるのです。

すると、部品の故障や発熱の原因になってしまいます。
そうならないように、波高率を指標としています。

その為、交流電源などには波高率が明記してあったりします。
波高率は低いほうが良いとだけでも覚えておきましょう。

以上、「正弦波交流の平均値・実効値・波高率・波形率の関係」についての説明でした。