【基礎から学ぶコンデンサ】 電界と電束と電気力線の関係

今回は、「電界と電束と電気力線の関係」についての説明です。

１．ポイント

「磁界と磁束と磁力線の関係」と併せて考えると覚えやすいです。

２．電界とは？

「2つの点電荷に働く静電力(反発力・吸引力)の大きさF[Nニュートン]は、2つの電荷q₁とq₂の積に比例し、距離の2乗に反比例する」という関係が「静電気に関するクーロンの法則」でした。
この静電力が働く空間のことを電界または電場と呼びます。
要するに、電荷があればその周りは電界が存在するんですね。

図1のように+q[C]と+1[C]の電荷が存在した時、+1[C]の単位正電荷に働く力の大きさのことを電界の強さと呼びます。
量記号はE、単位は[V/mボルト毎メートル]です。

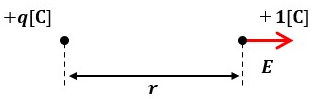
+1[C]の単位正電荷に働く静電力=電界の強さなので、電界の強さEを式で表すと以下のようになります。

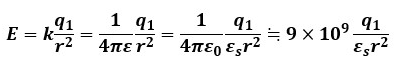
平たく言えば、静電力の大きさFを表す式の片側(ここではq₂)の電荷が+1[C]になっただけです。

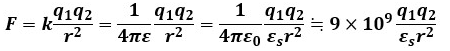
以上から、E[V/m]の電界中にq[C]の電荷を置いた時に電荷に働く静電力の大きさFは、F=qEと表せます。

３．電束とは？

電界は静電力の働く空間を指している為、抽象的でイメージがしづらいです。
その為、電界の様子を表すのに電束という仮想線を用います。
電束は量記号Ψサイ、単位は[C]です。

電束の性質は、以下のように定められています。

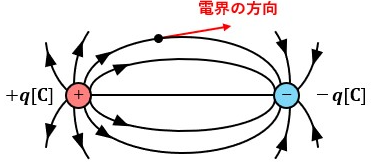
単位面積(1m²)当たりの電束を電束密度と呼びます。
量記号はD、単位は[C/m²クーロン毎平方メートル]です。
電束密度については、電気力線の説明の後の「５．電束密度と電気力線密度の関係」で触れます。

４．電気力線とは？

電束同様に、電界の様子を表すのに電気力線という仮想線を用います。

電束と電気力線は以下のような違いがあります。

電気力線は電界と密接な関係があります。
具体的に言うと、電気力線密度(単位面積当たりの電気力線の本数)=電界の強さEになるように定義されているので、電荷q[C]から出る電気力線数Nは、N=q/ε=q/ε₀ε_sとなります。
どういうことなのかを説明していきますね。

電界の強さは以下の通りでした。

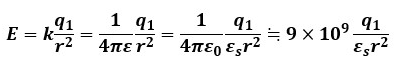
この式を変形すると以下のようになります。

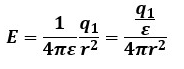
今、電荷q₁[C]を中心として距離r[m]の位置に球面があると考えます。

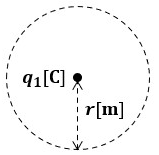
電荷q₁[C]からは立体的に電気力線がN本出ています。
この球体の表面積は4πr²です。
なので、電気力線密度(単位面積当たりの電気力線数)はN/4πr²と表せます。

ここで、電界の強さと電気力線密度を見比べてみましょう。

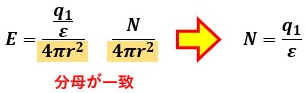
分母が球体の表面積で一致している為、電気力線数N=q₁/εの時に電界の強さ=電気力線密度という関係が成り立っていることがわかりました。

『そんな過程覚えられない！』って場合は図4のようなイメージを持ってもらえれば良いんじゃないですかね？

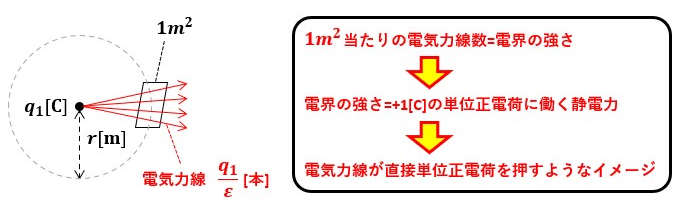
※ ここまでの話はあくまで覚え方の話で、電界の強さを先に定義したのか電気力線の本数を先に定義したのか私は良くわかっていません。

５．電束密度と電気力線密度の関係

電気力線密度(電界E[V/m])は単位面積当たりの電気力線数でした。

電束密度D[C/m²]は単位を見てわかるように、単位面積当たりの電荷です。
なので、電束密度も電気力線の時と同じように電荷q₁[C]を中心として距離r[m]の位置に球面があると考えると、以下のように表すことができます。

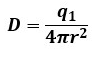
ここで、電束密度と電気力線密度(電界)を比較すると、D=εEという関係が導き出せるので、電気力線密度(電界)に誘電率を掛けると電束密度になることがわかります。

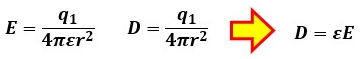
ちなみに、電束密度Dは上式の関係から、誘電率εに関係なく値が決定します。
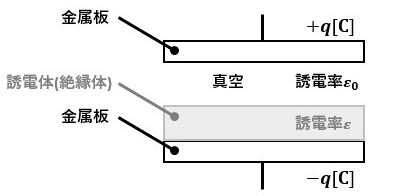
その為、図5のようにコンデンサの金属板間で誘電率が異なる箇所がある場合でも、常に電束密度は一定になります。
電束密度は一定でD=εEであることから、誘電率εが大きければその分電界の強さEが弱まります。

以上、「電界と電束と電気力線の関係」についての説明でした。

---