今回は、「復調」についての説明です。
1.ポイント
正弦波以外の交流波形のこと。
ひずみ波から元の情報を取り出して復元・調整すること。
2.ひずみ波の使用例
前回の記事でも説明していますが、改めて記載します。
周期性はあるけど正弦波ではないものをひずみ波と呼びます。
ひずみ波はいろんな周波数の波の塊というのは普通に理解できると思うのですが、そもそもひずみ波って何なのか疑問に持ちませんでしたか?
教科書に出てきたから一応覚えてはいるものの、どんなことに使用されているのかは謎という方は多いのではないでしょうか?
復調の説明に入る前にまずはそちらの補足説明から入ります。
電波などの情報は名前からわかる通り“波”です。
つまり、正弦波になっています。
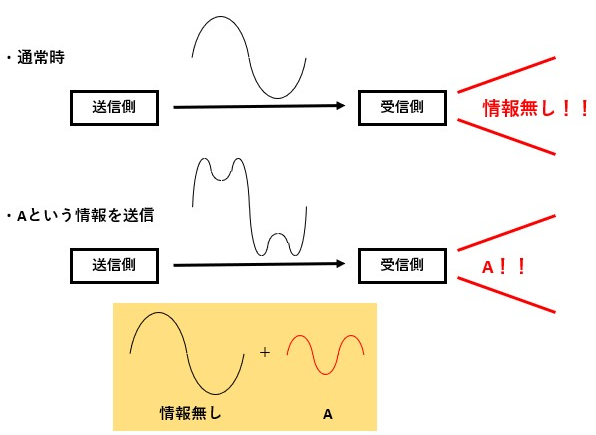
電波の送信側と受信側があるとすると、通常時はただの正弦波が送受信されています。
この正弦波が届いている場合は“何も情報が無い”としています。
この“何も情報が無い”を伝える波に伝えたい情報の波を載せることで、通常時とは異なる波形を検出してデータを受信したことを検知しつつ内容を確認しています。
つまり、情報を伝える場合は複数の正弦波が混ざり合った波になるわけです。
これがひずみ波となる場合があるということです。
この伝えたい情報の波のことを信号波もしくは変調信号、“何も情報が無い”を伝えている信号を載せる(キャリアする)ための波のことを搬送波・キャリア波、信号波と搬送波が合わさった波のことを変調波と呼びます。
そして、図1のように搬送波に信号波を乗せる操作を変調と呼びます。
例では描きやすいから搬送波の方を大きく・波長を長くしていますが、実際は搬送波の方が高周波になります。
この関係は、復調する際にコンデンサなどで構成した復調回路で搬送波を取り除くためのものです。
なぜ“何も情報が無い”ことを伝えているのかというと、おそらく問題無く通信できていることを相互に確認するための基準として扱っているのではないかと思います。
基準が無いと正常な情報なのかノイズなのかわからなそうですし。
3.復調とは?
通信の受信側がひずみ波を受け取りますが、伝えたい情報の波とひずみ波は当然波形が異なるので、この状態では何を伝えたいのかわかりません。
なので、このひずみ波の中から伝えたい情報の波を取り出す必要があります。
その為に、ひずみ波から搬送波(“何も情報が無い”を表す波)の成分を除去します。
そうすれば伝えたい状態の波だけ残り、情報が復元されるわけです。
このように、ひずみ波から元の情報を取り出して復元・調整することを復調と呼びます。
逆に、搬送波に情報を載せることを変調と呼びます。
復調と逆のことを変調と呼ぶということなのでセットで覚えてしまいましょう。
変調には様々な形式があるので、気になる方は以下の記事も参考にしてみてください。
4.ひずみ波から特定の周波数を取り出す方法
復調方法の一種として、ひずみ波からある周波数帯域の波を取り出す方法というものが存在します。
使う機会があるかは微妙なところですが、せっかくなのでまとめておきます。
今、cos8πt+cos12πtというひずみ波があったとします。
cos8πtはω=2πf=8πなので、周波数fは4[Hz]だとわかります。
同様に求めると、cos12πtは周波数fは6[Hz]です。
このひずみ波から周波数帯域1[Hz]の信号を取り出してみます。
方法は単純で、間の周波数の正弦波をかけるだけです。
この例の場合、4[Hz]と6[Hz]のひずみ波なので、5[Hz]の正弦波をかけることになります。
実際に計算してみますね。
(cos8πt+cos12πt)×cos10πt
=cos10πtcos8πt+cos12πtcos10πt
「三角関数の積和の公式」から、cosAcosB={cos(A+B)+cos(A-B)}/2なので、
{(cos18πt+cos2πt)+(cos22πt+cos2πt)}/2
=cos2πt+0.5cos18πt+0.5cos22πtとなります。
左から順番に1[Hz]、9[Hz]、11[Hz]の正弦波に復調することができました。
こういう考え方もある、程度の認識で良いと思います。
以上、「復調」についての説明でした。





